Шаг 1: находим координаты х точек перечечения графиков y=x^2+1 и y=-x+3.
x^2+1 = -x+3; x^2+x-2 = 0; x1 = -2; x2 = 1.
Шаг 2: Находим определенный интеграл функции y = -x+3 в пределах от -2 до 1.
Первообразная этой функции будет Y = -1/2*x^2 + 3x + С
Подставляя пределы интегрирования получаем площадь под функцией S1 = -1/2 + 3 + 2 + 6 = 10,5.
Шаг 3: Находим определенный интеграл функции y = x^2+1 в пределах от -2 до 1.
Первообразная этой функции будет Y = 1/3*x^3 + x + С
Подставляя пределы интегрирования получаем площадь под функцией S2 = 1/3 + 1 + 8/3 +2 = 6.
Шаг 4: S = S1-S2; S = 10,5-6; S = 4,5.
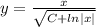
или так
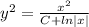
Пошаговое объяснение:
Найти общее решение дифференциального уравнения первого порядка.
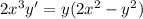
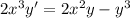
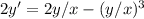
Получили однородное дифференциальное уравнение
Проводим замену приводящую к уравнению с разделяющимися переменными
у = xt(x) y’ = t + xt’
2(t + xt’) = 2t – t³
2xt’ = – t³
2t’/t³ = -1/x
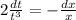
Интегрируем обе части уравнения
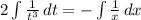
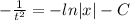
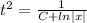
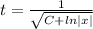
Находим переменную у
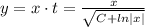
Получили общее решение диф. уравнения
Р=а+в+с ; Р=7см
а=1часть
в=2части
С=1ч:2=1/2части
Р= 1+2+1/2
Р=3 1/2 частей
7см=3 1/2частей
1ч= 7: 3 1/2
1ч= 7 : 7/2
1ч= 7 • 2/7
1ч= 1• 2/1= 2см это а сторона
а=2см; в= 2•2=4см; с=2:2=1см
ответ: стороны а=2см; в=4см; с=1см.
С икс
Р=7см
1ст=Х
2ст= 2Х
3ст=4Х
Х+2Х+4Х=7см
7Х=7
Х=7:7
Х=1см
Х=1см одна сторона
2Х=2•1=2см вторая сторона
4Х=4•1=4см третья сторона