a∈(-3/4; 1/2)
Пошаговое объяснение:
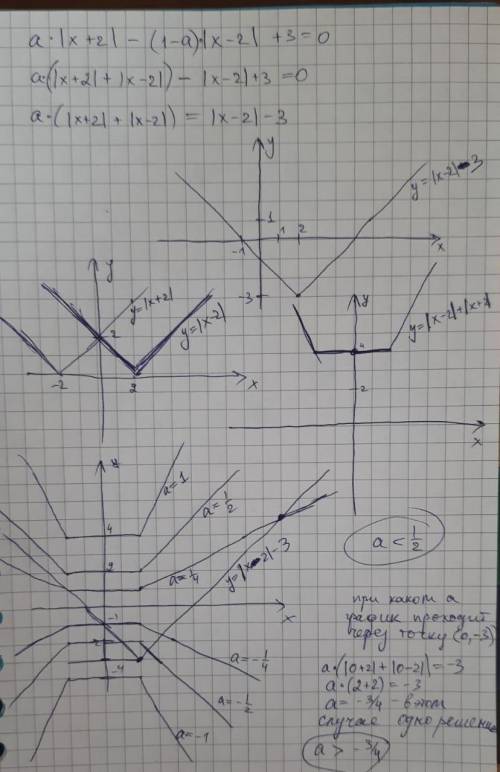
Прилагаю фото решения. Наверху преобрахование уравнения - уравниваю двае функции:
y₁=a(|x+2|+|x-2|)
y₂=|x-2|-3
Первый график - график y₁
Второй график - график вс для построения y₂ - график слагаемых |x+2| и |x-2|
Третий график - график y₂ в случае a=1
Четвертый график - изображение y₁ и разные варианты y₂, при разных значениях параметра а
а=1, а=1/2, а=1/4, а=-1/4, а=-1/2, а=-1 (при а=0 y₂ с осью Ox)
В случае a=1/2 крылья графика y₂ параллельны крыльям графика y₂ - значит они не пересекутся. (соответственно, решений не будет)
Как только мы сделаем a меньше, чем 1/2, наклон y₂ будет более пологий, чем у крыльев y₁ и значит крылья пересекутся - справа будет одно пересечение прямых и слева одно - значит будет два решения (например, смотри график при а=1/4
Теперь, каким может быть минимальное значение параметра а? (рассматриваем далее только значения a<1/2.)
В случае, который разбираю внизу справа на фото - это случай, когда вершина графика y₁ совпадет с правым углом y₂ - решаю уравнение и нахожу, что это происходит при а=-3/4 - в этом случае будет одно решение (x=2)
для всех больших значениях параметра решения будет два.
68 кг
Пошаговое объяснение:
Можно просто составить пропорцию:
170 (кг картофеля) относиться к X ( кг капусты) как пять относиться к двум.
Но, наверное, понятнее будет другой Всего есть 170 кг картофеля. Тогда если 170 разделить на 5 частей, мы узнаем сколько кг в одной девятой ( всего картофеля 5/9; если разделим весь вес картошки на пять частей, узнаем сколько весит одна девятая )
После этого нужно это число нужно умножить на два, и станет известно сколько капусты в килограммах завезли в магазин.
1) 170 : 5 = 34 (кг)
2) 34 * 2 = 68 (кг)
1-5 log^2(x)+6 log^2(x)^2<0
6 log^4(x)-5 log^2(x)+1<0
(2 log^2(x)-1) (3 log^2(x)-1)<0
(log^2(x)-1/2) (log^2(x)-1/3)<0
(log(x)-sqrt(1/2))*(log(x)+sqrt(1/2))*(log(x)-sqrt1/3)*(log(x)+sqrt1/3)<0
e^(-1/sqrt(2))<x<e^(-1/sqrt(3))
e^(1/sqrt(3))<x<e^(1/sqrt(2))
0,493069<x<0,561384
1,78131<x<2,02811
Как видим в этих промежутках целое число только одно - 2. ответ одно целое решение.