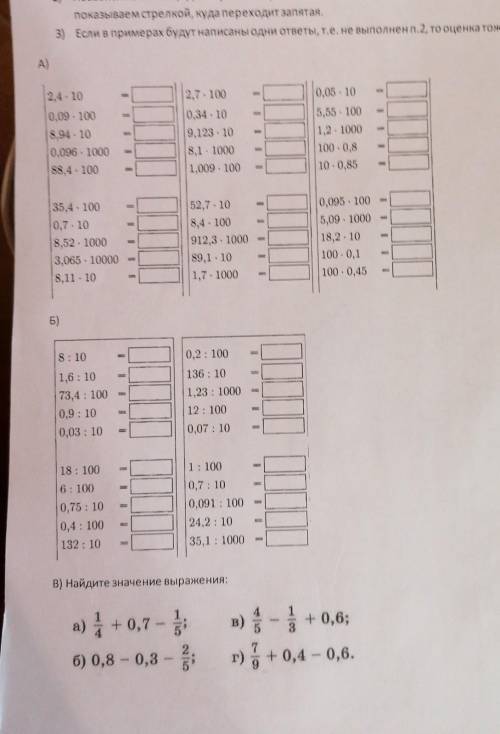
 , если
, если 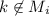 и
и 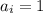 , если
, если 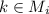 , где i=1,2,3. Назовем эту тройку сигнатурой разряда. Если для каких то двух разрядов c номерами k и m оказалось s(k)=s(m), то у Игоря нет никакой принципиальной возможности определить какая цифра в какой позиции находится. Поэтому количество цифр, которое может определить Игорь за 3 хода, не превосходит количества различных троек s(k), т.е. не превосходит 2³=8, и значит N≤8. И если Игорь хочет определять своими ходами максимальное количество разрядов, то ходы ему надо составлять так, чтобы каждой сигнатуре принадлежал только один разряд. и M₁∪M₂∪M₃ охватывало как можно больше разрядов. Если для какого-то разряда его сигнатура оказалась (0,0,0), т.е. этот разряд вообще не был затронут ходами Игоря, то определить цифру в этом разряде невозможно, т.к. цифр всего 10 и 10>8. Т.е. Игорь может определять цифры только в тех разрядах, которые принадлежат M₁∪M₂∪M₃. Значит N≤7. Покажем, что при N=7 множества M₁, M₂ и M₃ можно выбрать так, что каждой сигнатуре будет принадлежать только один разряд, и значит 7 цифр Игорь сможет всегда определить, например, с следующих ходов:
, где i=1,2,3. Назовем эту тройку сигнатурой разряда. Если для каких то двух разрядов c номерами k и m оказалось s(k)=s(m), то у Игоря нет никакой принципиальной возможности определить какая цифра в какой позиции находится. Поэтому количество цифр, которое может определить Игорь за 3 хода, не превосходит количества различных троек s(k), т.е. не превосходит 2³=8, и значит N≤8. И если Игорь хочет определять своими ходами максимальное количество разрядов, то ходы ему надо составлять так, чтобы каждой сигнатуре принадлежал только один разряд. и M₁∪M₂∪M₃ охватывало как можно больше разрядов. Если для какого-то разряда его сигнатура оказалась (0,0,0), т.е. этот разряд вообще не был затронут ходами Игоря, то определить цифру в этом разряде невозможно, т.к. цифр всего 10 и 10>8. Т.е. Игорь может определять цифры только в тех разрядах, которые принадлежат M₁∪M₂∪M₃. Значит N≤7. Покажем, что при N=7 множества M₁, M₂ и M₃ можно выбрать так, что каждой сигнатуре будет принадлежать только один разряд, и значит 7 цифр Игорь сможет всегда определить, например, с следующих ходов: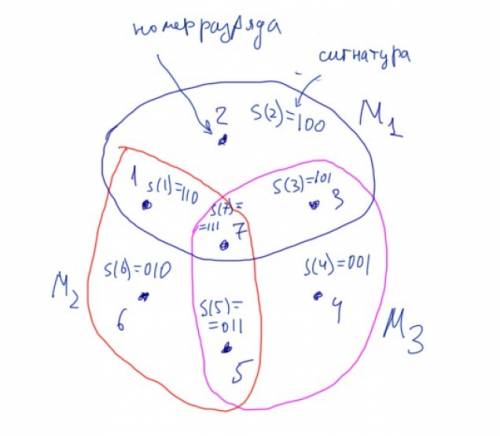
А)
1. 2.4*10=24
2. 0,09*100=9
3. 8,94*10=89,4
4. 0,096*1000=96
5. 2,7*100=270
6. 0,34*10= 3,4
7. 9,123*10= 91,23
8. 8,1*1000=8100
9. 1,009*100= 100,9
10. 0,05*10=0,5
11 .5,55*100 555
12. 1,2*1000= 1200
13. 100*0,8=80
14. 10*0,85= 8,5
15. 35.4*100= 3540
16. 0,7*10= 7
17. 8,52*1000= 8520
18. 3,065*10000= 30650
19. 8,11*10=81,1
20. 52.7*10= 527
21. 8,4*100=840
22. 912,3*1000=912 300
23. 89,1*10= 891
24. 1,7*1000=1700
25. 0,095*100=9,5
26. 5,09*1000=5090
27. 18,2*10=182
28. 100*0,1=10
29.100*0,45=45
Б) 1. 8:10=0,8
2. 1,6:10=0,16
3. 73,4:100=0,734
4. 0,9:10=0,09
5. 0,03:10=0,003
6. 0,2:100=0,002
7. 136:10= 13,6
8. 1,23:1000=0,00123
9. 12:100=0,12
10. 0,07:10=0,007
11. 18:100=0,18
12. 6:100=0,06
13. 0,75:100= 0,075
14. 0,4:100= 0,004
15. 132:10=13,2
16. 1:100=0,01
17. 0,091:100= 0,00091
18. 24,2:10= 2,42
19 35,1:1000= 0,0351