100 000 имеет 5 нулей. Закрываем сзади 5 цыфр. Открытыми остаются сотни тысяч.
55 сот.тысяч
2002002сот.тысяч
30303сот.тысяч
1.А) Уравнением называется равенство, содержащее одно или несколько неизвестных, значение которых необходимо найти.
2. верный ответ Значение переменной, при котором уравнение обращается в верное равенство.
среди предложенных не нашел.
3. линейным называют уравнение, в котором переменная /или переменные/ входят в первой степени, не равны нулю. можем еще так сказать
это уравнение вида ах+b=c
ax+by=c , где a, b, c - некоторые числа, х и у -переменные. причем а≠0, если речь об уравнении с двумя переменными, то а≠0;b≠0.
4. квадратное - это уравнение вида ах²+bx+c=0, где а,b,с - некоторые числа, причем а≠0, х и у-переменные.
5. Неравенство вида ах+b<0 (ах+b≤0, ах+b>0, ах+b≥0).где а≠0.
6. А) Уравнение имеет два равных действительных корня. но при условии, что решаем уравнение в области действительных чисел. иначе ответ Е.
7. А) Уравнение имеет два различных действительных корня. если речь о решении кв. уравнения в области действительных чисел.
иначе ответ Е.
8. А) Уравнение не имеет действительных корней.
9.D=b²-4ас
10. А) Уравнения, имеющие одно и то же множество решений
11. 7х-8=2х-3⇒А)х=1
12. 3-4х=5+8х⇒12х=-2, х=-1/6, верного ответа нет.
13. 7-х=-4+10х; х=1
14. 4х-4=6+3х⇒А)х=10
15. А) -0.5
16. 7-3х-3=х-1⇒А)1.25
17. -15+3х=2х-19⇒А)-4
18. 3-2х<5-3х⇒А) x<2
19. 5х+6>3х-2⇒А) x>-4
20. 3х-5≥23-4х⇒А) x≥4
21. По Виету А) 4;-2
22. 3х²-2х-1=0−1
здесь два ответа . ноль и 2/3
23. у=х+1 целая прямая ответов. подходят А, С,
24.- нет системы
25.аналогично.
26. аналогично
27 нет
28. 10х²-х+1=0 А) Не имеет действительных корней
29 нет уравнения
30нет неравенства. но больше половины, как требуют правила, я решил вам.
bb
Введу некоторые поправки: сумма начинается с n = 1.
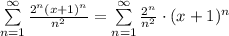
Степенной ряд в общем виде записывается следующим образом: 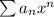 , где
, где 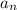 - формула числовых коэффициентов. Для данного ряда:
- формула числовых коэффициентов. Для данного ряда: 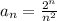 . Областью сходимости степенного ряда является интервал (-R;R), где R — радиус сходимости, определяемый соотношением:
. Областью сходимости степенного ряда является интервал (-R;R), где R — радиус сходимости, определяемый соотношением:
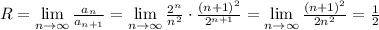
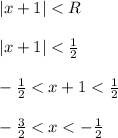
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу 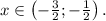 Теперь нужно проверить сходимость ряда на концах этого интервала.
Теперь нужно проверить сходимость ряда на концах этого интервала.
Если 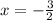 имеем
имеем 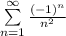 - числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
- числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
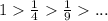
По второму признаку Лейбница предел ряда должен стремится к 0.
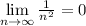
Второе условие Лейбница выполняется. Таким образом, предложенный рассматриваемый ряд сходится. Теперь нужно проверить на условной и абсолютной сходимости ряда. Возьмём ряд по модулю: 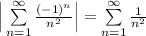 - сходящийся ряд. Следовательно, ряд
- сходящийся ряд. Следовательно, ряд 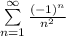 сходится абсолютно, значит
сходится абсолютно, значит 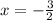 — точка сходимости.
— точка сходимости.
Аналогично, если 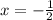 , имеем
, имеем 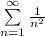 — сходящийся ряд. Следовательно,
— сходящийся ряд. Следовательно,
Таким образом, данный степенной ряд является сходящимся при ![x \in [-\frac{3}{2};-\frac{1}{2}].](/tpl/images/1356/8046/1421e.png)
в первом 500 сотен тысяч
во втором 2002002
а в третьем 30303