1) сколько песка загрузили?
7*8/9=56/9 т
2) сколько осталось после выгрузки на первом объекте?
7/7-2/7=5/7
56/9*5/7=40/9т=4 4/9 тонн осталось
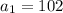
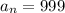
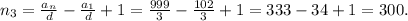
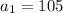

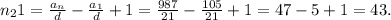
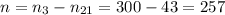 чисел.
чисел.
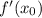
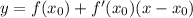

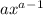 - где а- степень
- где а- степень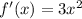 - вот такая вот производная
- вот такая вот производная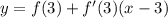
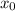 :
: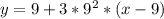
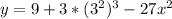
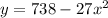
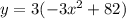 - это и есть касательная в ДАННОЙ точке.
- это и есть касательная в ДАННОЙ точке.
Загружен на 7* 8/9= 56/9 тонн
выгрузили 2/7 осталось 5/7
56/9 * 5/7= 280/63= 4 целых 4/9 тонны осталось