40+(20+20)=80
62-37=8+17
Пошаговое объяснение:
Пошаговое объяснение:
Задача №1
В белых рубашках- 2/5 учеников
В красных рубашках - 2/5 учеников
В синих рубашках - 6 учеников
Всего учеников - ?
Общее количество учеников примем за 1, тогда
2/5+2/5= 4/5 части составляли ученики в белых и красных рубашках
1-4/5= 5/5- 4/5=1/5 часть учеников была в синих рубашках.
по условию:
1/5 часть это 6 учеников
1 это х учеников
х=6:1/5= 6*5=30 учеников
ответ : на сцене было 30 учеников
Задача №2
1/6 от 2 мин., сколько секунд?
1 мин = 60 сек
2 мин=60*2=120 сек
120 сек.это 1 , тогда
120 сек - 1
х сек - 1/6
х= 120*1/6= 120/6=20 сек
ответ : 1/6 от 2 мин составит 20 сек
3/5 части от 1 года , сколько дней ?
1 год =365 дней
365 дней это 1, тогда
365 дней - 1
х дней - 3/5
х= 365*3/5= 219 дней
ответ 3/5 части от 1 года составит 219 дней
2/3 части от 1 года - сколько месяцев ?
1 год = 12 мес
12 мес это 1 , значит
12 мес . - 1
х мес. - 2/3
х= 12*2/3= 8 месяце
ответ : 2/3 части от 1 года составит 8 месяцев
ДАНО
Y= x/(1-x²)
ИССЛЕДОВАНИЕ
1.Область определения. Деление на 0 в знаменателе.
(1-x²) = (1-x)*(1+x)≠0. Разрыв функции при Х = +/- 1.
D(x) - Х∈(-∞;-1)∪(-1;1)∪(1;+∞).
Вертикальные асимптоты - X=-1 X=1.
2. Пересечение с осью Х. Y=0 при Х=0..
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.limY(-∞) = 0, limY(+∞) = 0
Горизонтальная асимптота - Y = 0.
5. Исследование на чётность.Y(-x) = - Y(x).
Функция нечётная.
6. Производная функции.
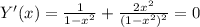
Корни при Х= +/- 1.
7. Локальные экстремумы.
Максимума и минимума – нет.
8. Интервалы монотонности.
Возрастает на всем интервале определения- Х∈(-∞;+∞)
9. Вторая производная - Y"(x).
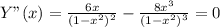
Корни производной - точки перегиба: х1 = 0,
9. Выпуклая “горка» Х∈(-1;0)∪(1;+∞), Вогнутая – «ложка» Х∈(-∞;-1)∪(0;1).
10. Область значений Е(у) У∈(-∞;+∞)
11. Наклонная асимптота. Уравнение: lim(∞)(k*x+b – f(x).
k=lim(∞)Y(x)/x = 0 - совпадает с горизонтальной
12.График в приложении
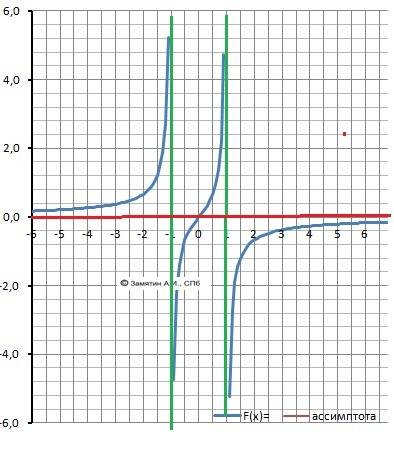
Пошаговое объяснение:
1. 20+
2+17