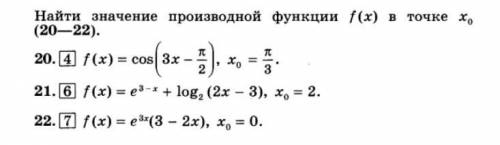
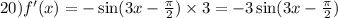
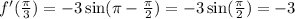
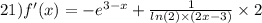
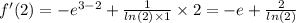
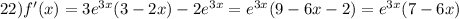
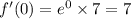
20. 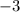
21. 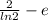
22. 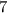
Пошаговое объяснение:
20. 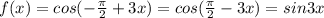
f'(x)=(sin3x)'=3cos(3x)
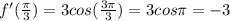
21. 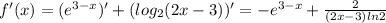
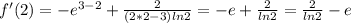
22. 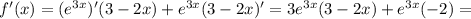
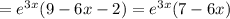
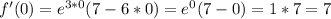
Пошаговое объяснение:
х- любое число
2) ни чет, ни нечет, непериодическая
3) нули функции: х= 2 кратность корня=2
и х=-1
4) производная= 3х квадрат-6х
крит точки
х= 0 и 2
Знаки производной
__+__0__-___2__+__
возрастает при х 0т бесконечности до 0 и от 2 до бесконечности
Убывает х от 0 до 2
х=0 максимум
х=2 минимум
у (макс) = 4
у (мин) = 0
4) Вторая производная = 6х-6
6(х-1)=0 при х=1- точка перегиба
- выпукла1+ вогнута
5) Поведение на бесконечности: если х---к минус бесконечность, то у--- -бесконечность
Если х--- +бесконечность, то у--- тоже к + бесконечность
1.Нахождение области определения функции
Определение интервалов, на которых функция существует.
!!! Очень подробно об области определения функций и примеры нахождения области определения тут.
2.Нули функции
Для вычисления нулей функции, необходимо приравнять заданную функцию к нулю и решить полученное уравнение. На графике это точки пересечения с осью ОХ.
3.Четность, нечетность функции
Функция четная, если y(-x) = y(x). Функция нечетная, если y(-x) = -y(x). Если функция четная – график функции симметричен относительно оси ординат (OY). Если функция нечетная – график функции симметричен относительно начала координат.
4.Промежутки знакопостоянства
Расстановка знаков на каждом из интервалов области определения. Функция положительна на интервале - график расположен выше оси абсцисс. Функция отрицательна - график ниже оси абсцисс.
5. Промежутки возрастания и убывания функции.
Для определения вычисляем первую производную, приравниваем ее к нулю. Полученные нули и точки области определения выносим на числовую прямую. Для каждого интервала определяем знак производной. Производная положительна - график функции возрастает, отрицательна - убывает.
6. Выпуклость, вогнутость.
Вычисляем вторую производную. Находим значения, в которых вторая производная равна нулю или не существует. Вторая производная положительна - график функции выпукл вверх. Отрицательна - график функции выпукл вниз.
7. Наклонные асимптоты.
Пример исследования функции и построения графика №1
Исследовать функцию средствами дифференциального исчисления и построить ее график.
Пошаговое объяснение: