Question

Определите вид квадратного уравнения, поставьте галочку в соответствующий столбец найдите корни неполных квадратных уравнений

Answer 1

1) неполное

2) неполное

3) приведенное

4) полное

5) полное

Пошаговое объяснение:

Неполным квадратным уравнением называют выражения вида:

$ax^{2} +bx=0$

$ax^{2} +c=0$

$ax^{2} =0$

$a,c,b$ - число, а $x$ - неизвестное

Полным квадратным уравнением называют выражение вида:

$ax^{2} +bx+c=0$

$a,c,b$ - число, а $x$ - неизвестное

Здесь слагаемые могут меняться местами, но этого смысл не изменится

Приведенным квадратным уравнением называют выражение вида:

$x^{2} +bx+c=0$

Числовой коэффициент, стоящий перед неизвестным с высшей степенью (степень - 2 или степень квадрата) должен быть равен 1

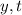Хочется отметить, что вместо латинской буквы $x$ могут выступать и другие буквы в качестве неизвестного ($y, t$ и так далее). Суть от этого не поменяется!