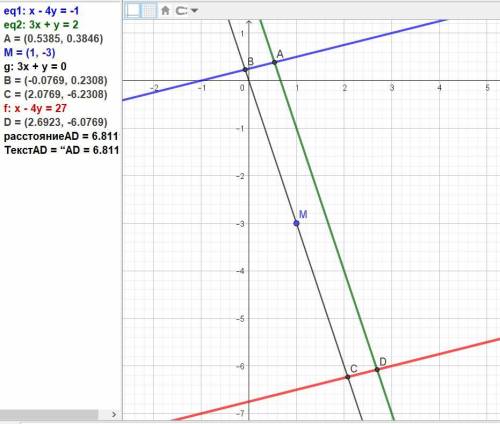
Уравнение прямой, включающей сторону ВС, найдём, подставив координаты точки М в уравнение с координатами переменных, как у параллельной прямой AD 3x + y – 2 = 0.
3*1 + (-3) + C = 0, отсюда С = -3 + 3 = 0.
Получаем уравнение BC: 3x + y = 0.
Находим вершину B параллелограмма как точку пересечения прямых АВ и ВС, решив систему:
{x – 4y + 1 = 0 x – 4y + 1 = 0
{3x + y = 0 (x4) = 12x + 4y = 0
13x + 1 = 0, x = -1/13,
y = – 3x = – 3(-1/13) = 3/13. Точка В((-1/13); (3/13)).
Находим точку С как симметричную точке В относительно точки М(1; -3).
х(С) = 2х(М) – х(В) = 2*1 - (-1/13) = 27/13,
y(С) = 2y(М) – y(В) = 2*(-3) - (3/13) = -81/13.
Уравнение прямой, включающей сторону CD, найдём, подставив координаты точки C в уравнение с координатами переменных, как у параллельной прямой AB x - 4y + 1 = 0.
(27/13) - 4(-81/13) + C = 0, отсюда С = (-27/13) – (324/13) = -351/13 = -27.
Получаем уравнение CD: x - 4y - 27 = 0.
S полн.= S осн + S бок
S осн = √(р·(р-а)(p-b)(p-c)) ,где р - полупериметр:
р= (a+ b+ c)/2 = (10+10+12)/2 = 16, тогда
S осн = √(р·(р-а)(p-b)(p-c))= √(16·6·6·4) =4·6·2= 48 ( см²).
2) Если боковые грани наклонены к плоскости основания под одним углом,
то площадь боковой поверхности равна половине произведения периметра
основания на высоту боковой грани: S бок = P осн·SH = 32·SH =...
Если боковые грани наклонены к плоскости основания под одним углом, то
в основание пирамиды можно вписать окружность, причём вершина пирамиды
проецируется в её центр, т.е. НО = r = Sосн/ p=48/16= 3 (см)
Из ΔSOH - прям.: L SHO = 45⁰, тогда L SHO = 45⁰, значит ΔSHO - равнобедрен.
и SO=ОН=3 см, SH = 3√2 см .
S бок = P осн·SH = 32·SH = 32·3√2 = 96√2 (см²)
Таким образом S полн = 48 + 96√2 = 48(1+ 2√2) (см²).