Пошаговое объяснение:
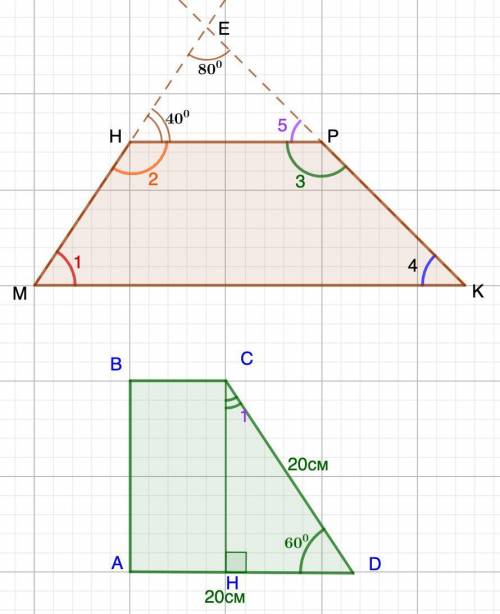
1. Дано: МНРК - трапеция.
МН ∩ РК = Е
∠МЕК=80°; ∠ЕНР=40°
Найти: углы трапеции.
1) Рассмотрим ΔНЕР.
Сумма углов треугольника равна 180°.⇒ ∠5=180°-(80°+40°)=60°
2) ∠ЕНР=∠1=40° - соответственные при НР║МК и секущей МЕ.
3)
Сумма смежных углов равна 180°.⇒ ∠2=180°-40°=140° - смежные.
4) ∠5=∠4 =60°- соответственные при НР║МК и секущей ЕК.
5) ∠3=180°-∠5=180°-60°=120° - смежные.
∠1=40°; ∠2=140°; ∠3=120°; ∠4=60°
2. Дано: АВСD - прямоугольная трапеция.
∠D = 60°;
АD=СD=20 см.
Найти: ВС.
1) Проведем высоту СН.
Рассмотрим ΔНСD - прямоугольный.
∠D = 60°
Сумма острых углов прямоугольного треугольника равна 90°.⇒ ∠1=90°-60°=30°.
Катет, лежащий против угла 30° равен половине гипотенузы.⇒ НD = СD:2=20:2=10 (см)
2) АН=АD-НD=20-10=10 (см)
3) Рассмотрим АВСН:
Если две прямые перпендикулярны третьей прямой, то они параллельны:СН⊥АD (построение)
АВ⊥АD (условие)
⇒ СН║АВ.
АВСН - параллелограмм.
Противоположные стороны параллелограмма равны.⇒ ВС=АН = 10 см.
SAFIR 471 61126Остаток: 113140 р. 1,80 x1,80 м. Добавить в корзинуКвадрат
ARABES 306 2224Остаток: 119380 р. 2,50 x2,50 м. Добавить в корзинуКвадрат
ISFAHAN 207 5542Остаток: 116250 р. 2,00 x2,00 м. Добавить в корзинуКвадрат
NAIN 305 1659Остаток: 216250 р. 2,00 x2,00 м. Добавить в корзинуКвадрат
DOFIN 209 5542Остаток: 216250 р. 2,00 x2,00 м. 2,50 x2,50 м. 3,00 x3,00 м. Добавить в корзинуКвадрат
ELITA R 352 3658Остаток: 116250 р. 2,00 x2,00 м. 2,50 x2,50 м. Добавить в корзинуКвадрат
ISFAHAN 207 63658Остаток: 325480 р. 2,50 x2,50 м. Добавить в корзинуКвадрат
SAFIR 471 60311Остаток: 19080 р. 1,50 x1,50 м. 2,40 x2,40 м. 3,00 x3,00 м. Добавить в корзину