Р = (a + b) · 2 = 28 дм - периметр прямоугольника
a + b = 28 : 2 = 14 дм - сумма длин ширины и длины
14 - 12 = 2 дм - ширина (b)
12 дм - длина (a)
а/b = 12/2 = 6/1 = 6 : 1 - отношение длины к ширине
b/a = 2/12 = 1/6 = 1 : 6 - отношение ширины к длине
6 к 1 - отношение длины к ширине
1 к 6 - отношение, обратное полученному
область определения функции: от минус бескорнечности до плюс бесконечности.пересечение с осью абсцисс (ox): x=0.0,x=2.82842712474619.3пересечение с осью ординат (oy): y=0. 4поведение функции на бесконечности: lim(xстремится к бесконечности)=минус бесконечность, lim(xстремится к минус бесконечности)=минус бесконечность.5исследование функции на четность/нечетность: четная функция.6производная функции равна: 8x-2.0x2.7нули производной: -2,0,2.8функция возрастает на: (минус бесконечность,-2]в объединении[0,2].9функция убывает на: [-2,0][2,бесконечность).10минимальное значение функции: минус бесконечность. 11максимальное значение функции: 8.0. а график посторить тут не смогу
Периметр прямоугольника равен удвоенной сумме его длины и ширины, то есть: . Пусть a - это длина прямоугольника, а b - его ширина. Выразим из выведенной формулы периметра ширину:
. Пусть a - это длина прямоугольника, а b - его ширина. Выразим из выведенной формулы периметра ширину:
Теперь мы можем найти отношение длины прямоугольника к его ширине, получаем:
Соответственно, обратное отношение равно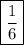 или 1 к 6.
или 1 к 6.