ответ в низу
Пошаговое объяснение:
Надеюсь
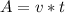 , где
, где 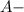 работа,
работа, 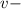 производительность, а
производительность, а 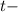 время.
время. . Тогда первому штукатуру понадобится вдвое больше времени, чем второму штукатуру, или
. Тогда первому штукатуру понадобится вдвое больше времени, чем второму штукатуру, или 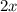 . Производительность первого штукатура -
. Производительность первого штукатура - 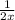 , а производительнось второго -
, а производительнось второго - 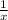 . Производительность обоих штукатуров равна
. Производительность обоих штукатуров равна 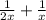 или
или 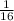 . Составим уравнение:
. Составим уравнение: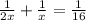
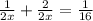
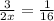
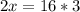
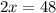
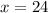
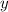 .
. 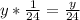 - работа второго штукатура. Так как оба штукатура работали 30 часов, то обозначим время первого штукатура за
- работа второго штукатура. Так как оба штукатура работали 30 часов, то обозначим время первого штукатура за 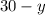 .
. 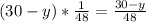 - работа первого штукатура. Работа обоих штукатуров равна
- работа первого штукатура. Работа обоих штукатуров равна 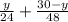 или
или  . Решим ещё одно уравнение:
. Решим ещё одно уравнение: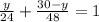
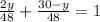
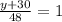
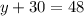
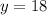
(2020 – 2019-1)(у – 3) – 2 = -2
Пошаговое объяснение: