у = 6 - x²; y = 0; x = 1; x = 3
6 - x² = 0 ⇒ x₁ = √6; x₂ = -√6
Ноль функции x₁ = √6 входит в интервал интегрирования
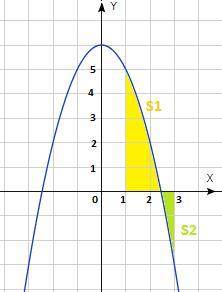
x₁ ∈ [1; 3] и разбивает криволинейную трапецию на 2 части : над осью Ох ( на графике залита жёлтым цветом ) и под осью Ох ( на графике залита зелёным цветом ). Общая площадь будет состоять из суммы двух площадей.
1) Площадь ограничена сверху параболой y = 6 - x², снизу осью абсцисс, слева прямой x = 1, справа нулём функции x₁ = √6.

2) Площадь ограничена снизу параболой y = 6 - x², сверху осью абсцисс, слева нулём функции x₁ = √6, справа прямой х = 3.
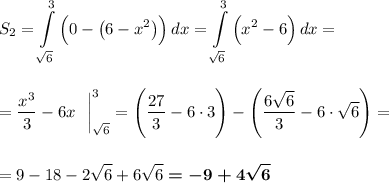
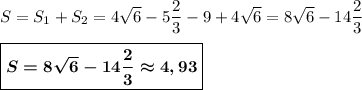
{3х-5у=23
{2х+3у=9
3х+2у=5х
-5у+3у=-2у
23+9=32
5х-2у=32
5х=32+2у
х=(32+2у)/5
3((32+2у)/5)-5у=23
у=-1
3х-5(-1)=23
х=6
{5х-2(у+4)=0
{6(2х+3)-у=41
5х-2у-8=0 12х+18-у=41 следовательно: 12х-у-23=0 5х+12х=17х -2у-у=-3у -8-23=-31 17х-3у=31 -3у=31-17х у=(31-17х)/-3 5х-2((31-17х)/-3)-8=0 х=2 у=1