Пошаговое объяснение:
22,5 м
Объяснение:
Скорость точки прямолинейного движения изменяется по закону
υ(t)=15·t-5·t² м/с.
Тогда из υ(t)=0 получаем t₀ - время начало движения и t₁ - время остановки:
15·t-5·t²=0 ⇔ 5·t·(3-t)=0 ⇔ t₀=0 и t₁=3.
Так как производная от пути S(t) равна скорости, то есть S'(t)=υ(t), определяем S(t) интегрированием:
S(t)=∫υ(t)dt=∫(15·t-5·t²)dt=15·t²/2 - 5·t³/3 + С.
В начале движения пройдённый путь равна нулю и поэтому:
S(t)=0 ⇔ 15·0²/2 - 5·0³/3 + С = 0 ⇔ С=0.
Значит S(t)=15·t²/2 - 5·t³/3. Тогда
S(3)=15·3²/2 - 5·3³/3=135/2 - 45=67,5-45=22,5 м.
килограммов (так как 
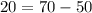). А вначале эта разница была равна 
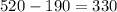килограммов.Значит, если 
часов, то разница стала равна 
. Это и будем использовать при решении задачи. a). Через 2 часа:
330 - 20 · 2 = 290 (кг)
b). Через 10 часов:
330 - 20 · 10 = 130 (кг)
c). Через 15 часов:
330 - 20 · 15 = 30 (кг)
d). Через 19 часов:
330 - 20 · 19 = - 50 (кг)
Как видим, через 19 часов муки уже будет больше на складе А.
Пошаговое объяснение:
а) Скорости теплохода по течению (a+b) км/ч
и против течения реки (a-b) км/ч
b) Расстояния, пройденного теплоходом по течению реки = 1,5*(a+b)
и против течения реки = 2*(a-b) км
c) Общего расстояния, пройденного теплоходом по течению реки и против течения реки = 1,5*(a+b) +2*(a-b) = 1,5a+1,5b+2a-2b=3,5a-0,5b км
d) Используя выражение из пункта (с), найдите его значение при а = 50 км/ч и b = 4 км/ч
3,5a-0,5b =3,5*50-0,5*4=175-2=173 км