Предположим, что весь центр куба 4х4х4 состоит из черных кубиков.
Тогда из них будет составлен куб 2х2х2 то есть всего - 8 кубиков.
Осталось: 32 - 8 = 24 черных кубика.
Минимальное количество черных плоскостей, размером 1х1 будет при расположении черных кубиков в центре каждой грани.
Всего в кубе 6 граней. Центр каждой составляет квадрат 2х2. То есть 4 черных квадратика в центре каждой грани. Всего 24.
Если мы сместим хотя бы один черный кубик на ребро или в угол куба, то количество черных квадратиков увеличится на 1 и на 2 соответственно.
Таким образом, минимальное количество черных квадратиков на поверхности данного куба - 24.
Так как каждая грань состоит из 16 квадратиков, то всего таких квадратиков на поверхности куба: 16 · 6 = 96.
Вычтем черные квадратики: 96 - 24 = 72 (белых квадратика 1х1)
ответ: 72.
ПОШАГОВОЕ ОБЪЯСНЕНИЕ:
1) В одном сантиметре 10 миллиметров (1 см = 10 мм).
2) Два разных отрезка, длина каждого из которых больше 8 см и меньше 9 см — это означает, что
допустимая длина для каждого отрезка — от 8 см 1 мм до 8 см 9 мм.длины отрезков не должны быть одинаковыми.3) Теперь скажу то же самое, но подробнее:
Длина каждого из отрезков больше 8 см и меньше 9 см — это означает, что один из отрезков может иметь длину:
8 см 1 мм, 8 см 2 мм, 8 см 3 мм, 8 см 4 мм, 8 см 5 мм, 8 см 6 мм, 8 см 7 мм, 8 см 8 мм, 8 см 9 мм.При этом оба отрезка должны иметь разную длину. Например, можно начертить отрезки длиной 8 см 5 мм и 8 см 7 мм.
4) Отрезок имеет начало и конец, поэтому начало и конец отрезка нужно обозначить чёрточками.
ПРИМЕР РЕШЕНИЯ:
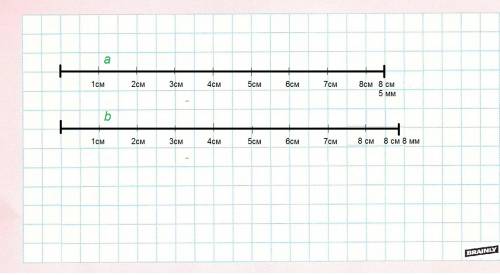
Начертим два отрезка. Пусть длина первого отрезка равна 8 см 5 мм, а длина второго — 8 см 8 мм. Обозначим отрезки буквами a и b.
(картинка с отрезками прикреплена к ответу)
-----------------------
Можно взять любые две длины отрезков. Главное, чтобы длины отрезков не были одинаковыми (чтобы длины были разными) и чтобы длина каждого при этом была больше 8 см и меньше 9 см.
Надеюсь, всё понятно.
Дана функция f(x)=4x³+x²-2x-6.
Её производная равна: y' = 12x²+2x-2.
Приравняем производную нулю: 12x²+2x-2 = 0, 2(6x²+x-1) = 0.
Д = 1+24 = 25, х1 = (-1-5)/12 = -1/2, х2 = (-1 + 5)/12 = 4/12 = 1/3.
Найдены 2 критические точки: х1 = (-1/2) и х2 =(1/3).
Находим значения производной на полученных промежутках:
х ∈ ( -∞;(-1/2) ) ((-1/2);(1/3)) ((1/3);+∞).
х = -1 (-1/2) 0 ( 1/3) 1
y' = 8 0 -2 0 12.
Ф_ция ↑ max ↓ min ↑
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.