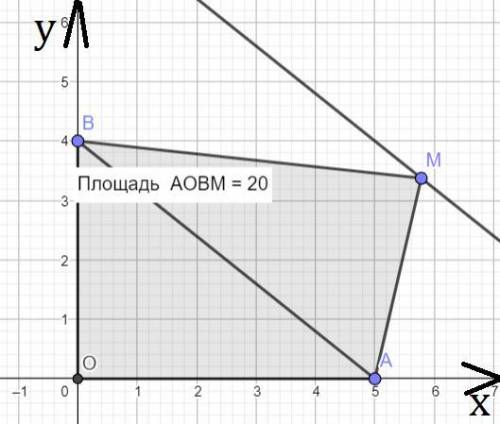
Прямая проходящая через точки A, B имеет уравнение:
y=ax+t, подставим координаты точек чтобы найти уравнение в явном виде.
4=a·o+t ⇒ t=4; 0=a·5+t ⇒ a=-4/5=-0,8
Исходя из последовательности вершин четырёхугольника, получаем, что координаты M(x;y) удовлетворяют неравенству y≥-0,8x+4.
Заметим, что S(AOBM) = S(AOB)+S(BMA), при этом S(AOBM)=20, S(AOB)=AO·OB/2=10.
Тогда S(BMA)=10.
Поскольку площадь треугольника постоянная и длина стороны AB тоже. То высота опущенная из M на AB должна быть постоянной, откуда M лежит на прямой параллельной AB. Тогда угол наклона k равен углу наклона прямой проходящей через точки A, B.
k = -0,8
ответ: -0,8.
Прямая проходящая через точки A, B имеет уравнение:
y=ax+t, подставим координаты точек чтобы найти уравнение в явном виде.
4=a·o+t ⇒ t=4; 0=a·5+t ⇒ a=-4/5=-0,8
Исходя из последовательности вершин четырёхугольника, получаем, что координаты M(x;y) удовлетворяют неравенству y≥-0,8x+4.
Заметим, что S(AOBM) = S(AOB)+S(BMA), при этом S(AOBM)=20, S(AOB)=AO·OB/2=10.
Тогда S(BMA)=10.
Поскольку площадь треугольника постоянная и длина стороны AB тоже. То высота опущенная из M на AB должна быть постоянной, откуда M лежит на прямой параллельной AB. Тогда угол наклона k равен углу наклона прямой проходящей через точки A, B.
k = -0,8
ответ: -0,8.
Пошаговое объяснение:
Школьные Знания.com
Какой у тебя вопрос?
Marinochka28
мария559
09.01.2016
Математика
5 - 9 классы
ответ дан • проверенный экспертом
выберите тождественно равные выражения .запишите их в виде тождества. 1)(а-а)×b и0 2)(x+y)×0 и x+y 3)5,1x7 и 35,7x 4)a-b и b- a 5)x-y и (y-x)(-1) 6)7(a-b) и 7а-7b
1
СМОТРЕТЬ ОТВЕТ
ответ, проверенный экспертом
4,0/5
171
ashtvortz
отличник
363 ответов
165 тыс. пользователей, получивших
Классическое определение гласит, что “два выражения, значения которых равны при любых значениях переменных, называются тождественно равными, а тождество – это равенство, верное при любых значениях переменных”. Исходя из этого определения, в приведенных выражениях определены такие тождества:
1) (а - а) × b = 0 — тождество, т.к. (а-а) при любых значениях равно нулю, а любое число, умноженное на ноль, всегда даёт ноль;
2) (x + y) × 0 и x + y — выражения не тождественно равны, т.к. любое число, умноженное на ноль, всегда даёт ноль, а x + y может отличаться от нуля;
3) 5,1x7 = 35,7x — тождество, т.к. (5,1×7= 35,7) при любых значениях х;
4) a - b и b - a — выражения не тождественно равны, т.к. a в общем случае не равно b;
5) x - y = (y - x)(-1) — тождество, т.к. (y - x)(-1) после раскрытия скобок преобразуется в x - y;
6) 7(a - b) = 7а - 7b — тождество, т.к. 7а - 7b после вынесения за скобки общего множителя преобразуется в 7(a - b).