В решении.
Пошаговое объяснение:
1) |5-2х|<-10
↓
5 - 2х < -10 5 - 2x > 10
-2х < -10 - 5 -2х > 10 - 5
-2х < -15 -2x > 5
2x > 15 2x < -5 знак неравенства меняется при делении на минус;
x₁ > 7,5; x₂ < -2,5.
Но х₁ не удовлетворяет второму неравенству, а х₂ не удовлетворяет первому неравенству.
Данное неравенство не имеет решения.
2) |х+2|<3
↓
х + 2 < 3 x + 2 > -3
x < 3 - 2 x > -3 - 2
x₁ < 1; x₂ > -5;
Решения неравенства: х∈(-5; 1).
Неравенство строгое, скобки круглые.
3) |1-2х|≤5
↓
1 - 2х <= 5 1 - 2x >= -5
-2x <= 5 - 1 -2x >= -5 - 1
-2x <= 4 -2x >= -6
2x >= -4 2x <= 6 знак неравенства меняется при делении на минус;
x₁ >= -2; x₂ <= 3;
Решения неравенства: х∈[-2; 3].
Неравенство нестрогое, скобки квадратные.
4) |4х-3|>10
↓
4x - 3 > 10 4x - 3 < -10
4x > 10 + 3 4x < -10 + 3
4x > 13 4x < -7
x₁ > 13/4; x₂ < -7/4;
Решения неравенства: х∈(-∞; -7/4)∪(13/4; +∞).
Неравенство строгое, скобки круглые.
5) |-х+1|>-2,1
↓
-х + 1 > -2,1 -x + 1 < 2,1
-x > -2,1 - 1 -x < 2,1 - 1
-x > -3,1 -x < 1,1
x₁ < 3,1; x₂ > -1,1; знак неравенства меняется при делении на минус;
Решения неравенства: х∈(-1,1; 3,1).
Неравенство строгое, скобки круглые.
Для начала нужна понять, что цифра Г в слове ГАВ, будет означать сотни, А десятки и В единицы. Это мне кажется понять как решать такие задачи.
ГАВ+ГАВ+ГАВ = ВВВ + 48
Сразу можно заметить, что Г и В не могут быть равны нулю, так как есть числа, где они стоят впереди
преобразуем в другой вид
3*ГАВ = ВВВ + 48
3 * (Г*100 + А*10 + В) = В*100 + В*10 + В + 48
300*Г + 30*А + 3*В = 111*В + 48
300*Г + 30*А - 108*В = 48
30*ГА - 108*В = 48
10*ГА - 36*В = 16
5*ГА - 8 = 18*В
5*ГА = 18*В + 8
Будем постепенно увеличивать В, и записывать те значения, где 18*В + 18 будет кратно 5.
Этими значениями будут 4 и 9.
Составим и решим уравнения, чтобы найти какие значения которые могут принимать Г и А.
5*ГА = 80, где Г ≠ 0;4;A A ≠ 4;Г В ≠ 0;Г;А
ГА = 16
значит Г = 1; А = 6; В = 4
5*ГА = 170, где Г ≠ 0;9;A A ≠ 9;Г В ≠ 0;Г;А
ГА = 34
значит Г = 3; А = 4; В = 9
ответ: 164 и 349
Пусть данные числа a и b, тогда по условию
a > 0
b > 0
то есть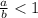
0 < a < b
тогда b - a = 0,85 (по условию)
b = a + 0,85.
решаем уравнение для нахождения a
a·7 = 2·(a+0,85)
7a = 2a + 2·0,85
7a - 2a = 1,7
5a = 1,7
b = a + 0,85 = 0,34 + 0,85 = 1,19.
ответ. 0,34 и 1,19.