Предположим, что указанное свойство было выполнено. Представим болельщиков в виде вершин графа, а их знакомства - в виде рёбер. Группой вершин степени k назовём множество всех вершин степени k. По условию задачи в группе вершин степени k будет ровно k вершин. Если k чётно, то сумма степеней вершин в группе тоже чётна, а если k нечётно, то сумма степеней группы нечётна. Так как 2015 - нечётное число, групп с нечётным k будет нечётное число, что означает, что сумма степеней всех вершин нечётна, что неверно, так как сумма степеней всех вершин любого графа чётна.
ответ: Не могло.
Пошаговое объяснение:
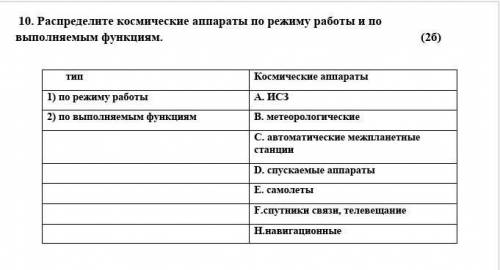
Тип Космические аппараты/функции
1 по режиму работы: ИСЗ, автоматические межпланетные станции, спускаемые аппараты, самолеты
2 по выполняемым функциям: Метеорологические. спутники связи, телевещание, навигационные