Найдем количество благоприятных нам исходов. Первый человек может родиться в любой из 12 месяцев. Чтобы дни рождения всех четырех людей приходились на разные месяца, второй должен родиться в любой из 11 оставшихся месяцев, третий - в любой из 10, и четвертый - в любой из 9. Таким образом, есть 12 · 11 · 10 · 9 благоприятных исходов.
Несложно убедиться, что всего исходов 12⁴ (так как день рождения у каждого может быть в любой из 12 месяцев).
Считаем искомую вероятность как отношение благоприятных исходов ко всем возможным исходам: 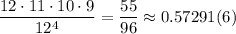
ответ: 55/96
x ∈ (-∞;-4) ∪ (-1;3)
Пошаговое объяснение:
(x-3)(x+1)(x+4)<0
Это возможно, если нечетное количество множителей отрицательно. Т.е. возможны такие варианты
один множитель отрицательный:
1. x-3>0; x>3; x∈(3;+∞)
x+1>0; x>-1; x∈(-1;+∞)
x+4<0 x<-4; x∈(-∞;-4)
x∈∅
2. x-3<0; x<3; x∈(-∞;3)
x+1>0; x>-1; x∈(-1;+∞)
x+4>0 x>-4; x∈(-4;+∞)
x∈(-1;3);
3. x-3<0; x>3; x∈(3;+∞)
x+1>0; x<-1; x∈(-∞;-1)
x+4>0 x>-4; x∈(-4;+∞)
x∈∅
все три множителя отрицательные:
4. x-3<0; x<3; x∈(-∞;3)
x+1>0; x<-1; x∈(-∞;-1)
x+4>0 x<-4; x∈(-∞;-4)
x∈(-∞;-4);
Окончательно:
x ∈ (-∞;-4) ∪ (-1;3)
1) 6,1 6,5 6,09
2)2,4 2,55 2,78
3)9,9 9,01 9,6
4) 11,2 11,101 11,65