V=1/3пH(R1в квадрате + R1*R2 + R2 в квадрате) . Радиусы нам известны R1=10 R2=6. Нам нужно узнать только высоту. рассмотрим треугольник СКД , где угол СДК=60, СК-высота, проведенная из вершины С. СК-искомая высота. рассмотрим трапецию АБСД. (БН- высота, проведенная из вершины Б) НК=БС( т.к трапеция равнобедренная) пусть АН= КД=х. Тогда х+ 2*R1 +x=2*R2. 2х+12=20. 2х=8. х=4. в тругольнике СКД выразим тангенс угла в 60 градусов. tg60=СК/КД. СК=(корень из 3)*4. V=1/3*п* (корень из 3)*4 *(36 + 60 +100)= 784/3*п* корень из 3
20
Пошаговое объяснение:
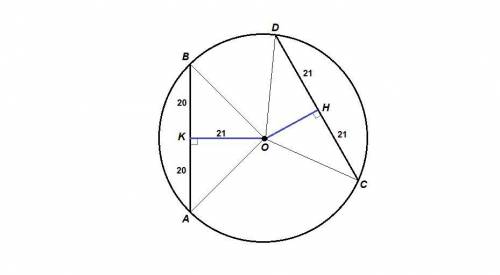
Соединим центр окружности с концами хорд.
ОА = ОВ = ОС = OD как радиусы.
Проведем ОК⊥АВ и и OH⊥CD,
ОК = 21 - расстояние от центра до АВ,
ОН - искомое расстояние от центра до CD.
ΔОАВ равнобедренный, значит ОК - высота и медиана. ⇒
АК = КВ = 1/2АВ = 1/2 · 40 = 20
Из прямоугольного треугольника АКО по теореме Пифагора:
АО = √(АК² + КО²) = √(20² + 21²) = √(400 + 441) = √841 = 29
СО = АО = 29
ΔCOD равнобедренный, значит OН - высота и медиана, ⇒
СН = HD = 1/2CD = 1/2 · 42 = 21
Из прямоугольного треугольника СОН по теореме Пифагора:
OH = √(CO² - CH²) = √(29² - 21²) = √(841 - 441) = √400 = 20
Вот так...
Пошаговое объяснение: