66км
Пошаговое объяснение:
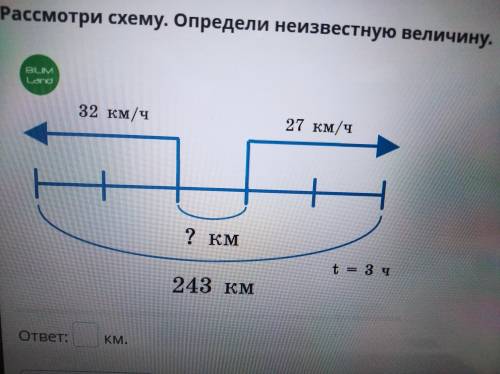
32+27=59
59*3=177
243-177=66км
Все 4 функции вида y = kx + b. если b > 0, то прямая соприкасается с осью ординат выше оси абсцисс, а если b < 0, то прямая соприкасается с осью ординат ниже оси абсцисс.
Значит, графики A и B соответствуют уравнениям 2 и 3, а графики C и D соответствуют уравнениям 1 и 4. Определим теперь конкретно какой график к какому уравнению подходит.
Рассмотрим уравнение, в котором k = 2
y = 2x + 5, причём x = = 2,5. Значит, прямая проходит через точку абсцисс 2,5.
Рассмотрим уравнение, в котором k = 1
y = x - 5, из свойств числового коэффициента b следует, что график проходит через точку ординат -5, а из формулы y = a(x - m)² следует, что точка соприкосновения оси абсцисс и прямой смещена вправо на 5.
Проведя аналогичные рассуждения с остальными двумя уравнениями и их графиками, придём к выводу, что
Пошаговое объяснение:
1) - C
2) - A
3) - B
4) - D
Даны координаты вершин пирамиды АВСD :
А(-5;-1;8), В(2;3;1), С(4;1;-2), D(6;3;7).
Найти: 1. Длину | вектор |АВ| = √((2-(-5))² + (3-(-1))² + (1-8)²) =
√(49 + 16 + 49) = √114 ≈ 10,67708.
2. Величину угла между векторами АВ и АС.
Вектор АВ = (7; 4; -7) определён в п. 1. Модуль = √114 ≈ 10,67708.
Вектор АС = (9; 2; -10), √(81+4+100) = √185 ≈ 13,60147.
cos(AB_AC) = (7*9+4*2+(-7)*(-10))/(√114*√185) = 141/√21090 =
= 141/145,223965 ≈ 0,970914133 .
Угол равен arc cos (141/√21090) = 0,241777 радиан или 13,85278 градуса.
3. Площадь грани АСD,
Находим векторы АС и АD.
Вектор АC = (9; 2; -10) определён в п. 1. Модуль = √185 ≈ 13,60147.
Вектор АD = (11; 4; -1), √(121+16+1) = √138 ≈ 11,74734.
Площадь грани ACD равна половине модуля векторного произведения: S = (1/2)|AC*AD|.
i j k| i j
9 2 -10| 9 2
11 4 -1| 11 4 = -2i - 110j + 36k + 9j + 40i - 22k =
= 38i - 101j + 14k = (38; -101; 14).
Модуль равен √(38² + (-101)² + 14²) = √11841 ≈ 108,8163591 .
Площадь S = (1/2)*√11841 = 54,40817953 .
4. Объем АВСD(объем пирамиды ).
Объём пирамиды V = (1/6)*|(ABxAC)*AD|.
Вектор АВ = (7; 4; -7) определён в п. 1. Модуль = √114 ≈ 10,67708.
Вектор АС = (9; 2; -10), √(81+4+100) = √185 ≈ 13,60147. (см. п. 2).
i j k| i j
7 4 -7| 7 4
9 2 -10| 9 2 = -40i - 63j + 14k + 70j +1 4i - 36k =
= -26i + 7j - 22k = (-26; 7; -22).
Модуль равен √((-26)² + 7² + (-22)²) = √1209 ≈ 34,7706773 .
5. Уравнение стороны ВС. Вектор ВС = (2; -2; -3).
(x - 2)/2 = (y - 3)/(-2) = (z - 1)/(-3).
6. Уравнение грани АВD по точкам А(-5;-1;8), В(2;3;1), D(6;3;7).
Для составления уравнения плоскости используем формулу:
x - xA y - yA z - zA
xB - xA yB - yA zB - zA
xC - xA yC - yA zC - zA
= 0
Подставим данные и упростим выражение:
x - (-5) y - (-1) z - 8
2 - (-5) 3 - (-1) 1 - 8
6 - (-5) 3 - (-1) 7 - 8
= 0
x - (-5) y - (-1) z - 8
7 4 -7
11 4 -1
= 0
x - (-5) 4·(-1)-(-7)·4 - y - (-1) 7·(-1)-(-7)·11 + z - 8 7·4-4·11 = 0
24 x - (-5) + (-70) y - (-1) + (-16) z - 8 = 0
24x - 70y - 16z + 178 = 0 или, сократив на 2
12x - 35y - 8z + 89 = 0 .
7.Уравнение высоты СН к грани АВD .
Нормальный вектор плоскости АВД принимаем из её уравнения:
АВД = (12; -35; -8).
Тогда уравнение высоты СН:
(x - 4)/12 = (y - 1)/(-35) = (z + 2)/(-8).
78 км/ч
Пошаговое объяснение:
52 + 30 = 82
82 * 2 = 164
320 - 164 = 156
156 : 2 = 78