Пусть требуемое в задаче возможно и в ящике есть ("маленьких") фруктов меньше грамм. Тогда ("больших") фруктов, чья масса больше
С одной стороны, масса всех фруктов равна , а с другой стороны - . Но так как мы говорим об одной и той же группе фруктов, то:
Но в задаче сказано, что "есть как минимум различных по массе фрукта". Но полученный в этом случае результат противоречит условию Из этого заключаем, что описанная ситуация невозможна.
ответ: нет, не может.
б).
Пусть есть "маленьких" фруктов и "больших" (в этом случае "средних" фруктов будет ). Точно также, как и в пункте, составим уравнение:
Мы получили очень интересный результат: в любом случае отношение количества "маленьких" и "больших" фруктов будет равно .
Значит, так как и обязательно должны быть натуральными, общее число "маленьких" и "больших" фруктов должно делиться на . Такое общее число будет обязательно меньше или равно .
Получается, что количество "средних" фруктов больше или равно . В ящике их уж никак не может быть.
ответ: нет, не может.
в).
Так как в задаче сказано "найдите наибольшую возможную массу фрукта", то наверняка нужно считать массы фруктов целыми числами.
Если есть "больших" фруктов и - масса наибольшего,то, чтобы "понизить" значение среднего арифметического (и привести его в итоге к числу ), нужно массу остальных "больших" фруктов сделать как можно меньше - в районе грамма.
Поэтому:
Как было фактически выяснено в пункте задачи, максимальное значение равно (а максимальное при максимальном значении ).
Делаем вывод, что в этом случае:
.
Теперь проверим, что этот случай нам действительно подходит:
Есть "больших" фруктов: масса из них равна , а масса составляет граммов.Есть "маленьких" фруктов: масса каждого - по граммов.И еще "средних" фруктов, ровно по граммов.
Кол-во вариантов взять 6 карт: первая Любая из 36 Вторая Любая из оставшихся 35 Третья Любая из оставшихся 34 Четвертая Любая из оставшихся 33 Пятая Любая из оставшихся 32 Шестая Любая из оставшихся 31
И нужно разделить на кол-во перестановок внутри этих шести карт Итак получаем 36*35*34*33*32*31/(6*5*4*3*2)
Кол-во вариантов взять из этих шести карт чтобы среди них было 4 туза На первое место - туз На второе место - туз На третье место - туз На четвертое место - туз Н пятое место любую из оставшихся 32 На шестое место любую из оставшихся 31 И разделить на кол-во перестановок внутри этих шести карт Получается 1*1*1*1*32*31/(6*5*4*3*2)
а).Пусть требуемое в задаче возможно и в ящике есть ("маленьких") фруктов меньше
("маленьких") фруктов меньше 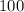 грамм. Тогда ("больших") фруктов, чья масса больше
грамм. Тогда ("больших") фруктов, чья масса больше
С одной стороны, масса всех фруктов равна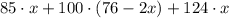 , а с другой стороны -
, а с другой стороны - 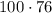 . Но так как мы говорим об одной и той же группе фруктов, то:
. Но так как мы говорим об одной и той же группе фруктов, то:
Но в задаче сказано, что "есть как минимум различных по массе фрукта". Но полученный в этом случае результат противоречит условию Из этого заключаем, что описанная ситуация невозможна.
различных по массе фрукта". Но полученный в этом случае результат противоречит условию Из этого заключаем, что описанная ситуация невозможна.
ответ: нет, не может.
б).Пусть есть "маленьких" фруктов и
"маленьких" фруктов и 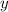 "больших" (в этом случае "средних" фруктов будет
"больших" (в этом случае "средних" фруктов будет 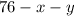 ). Точно также, как и в пункте, составим уравнение:
). Точно также, как и в пункте, составим уравнение:
Мы получили очень интересный результат: в любом случае отношение количества "маленьких" и "больших" фруктов будет равно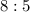 .
.
Значит, так как и
и 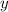 обязательно должны быть натуральными, общее число "маленьких" и "больших" фруктов должно делиться на
обязательно должны быть натуральными, общее число "маленьких" и "больших" фруктов должно делиться на 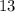 . Такое общее число будет обязательно меньше или равно
. Такое общее число будет обязательно меньше или равно 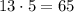 .
.
Получается, что количество "средних" фруктов больше или равно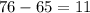 . В ящике их
. В ящике их 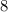 уж никак не может быть.
уж никак не может быть.
ответ: нет, не может.
в).Так как в задаче сказано "найдите наибольшую возможную массу фрукта", то наверняка нужно считать массы фруктов целыми числами.
Если есть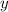 "больших" фруктов и
"больших" фруктов и 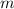 - масса наибольшего,то, чтобы "понизить" значение среднего арифметического (и привести его в итоге к числу
- масса наибольшего,то, чтобы "понизить" значение среднего арифметического (и привести его в итоге к числу 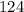 ), нужно массу остальных "больших" фруктов сделать как можно меньше - в районе
), нужно массу остальных "больших" фруктов сделать как можно меньше - в районе 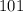 грамма.
грамма.
Поэтому:
Как было фактически выяснено в пункте задачи, максимальное значение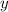 равно
равно 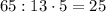 (а
(а 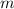 максимальное при максимальном значении
максимальное при максимальном значении 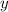 ).
).
Делаем вывод, что в этом случае:
Теперь проверим, что этот случай нам действительно подходит:
ЕстьСредняя масса "больших":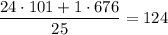 .
.
Средняя масса "средних":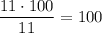 .
.
Средняя масса "маленьких":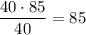 .
.
Общая средняя масса: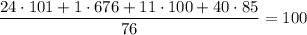 .
.
Все сходится!
ответ: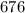 граммов.
граммов.