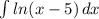
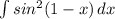
ответ: x=11/7, y=9/7, z=2/7.
Пошаговое объяснение:
Перепишем систему так:
-z -y + x=0
-3z +y + x=2
3y+2x=7
Прямой ход метода Гаусса.
1) Умножим первое уравнение на -3, сложим его со вторым и заменим второе уравнение полученной суммой. Придём к системе:
3z+3y-3x=0
4y-2x=2
3y+2x=7
2) Умножим второе уравнение на 3, третье - на 4, вычтем из второго уравнения третье и заменим третье уравнение полученной разностью. Придём к системе:
3z+3y-3x=0
12y-6x=6
-14x=-22
На этом прямой ход метода Гаусса заканчивается и начинается
Обратный ход метода Гаусса.
1) Из третьего уравнения находим x=22/14=11/7
2) Подставляя это значение во второе уравнение, находим y=9/7
3) Подставляя найденные значения x и y в первое уравнение, находим z=2/7.
Проверка:
11/7-9/7-2/7=0
11/7+9/7-6/7=2
22/7+27/7=7
Пошаговое объяснение:
1) 1. (-3 1/4 +2 1/6)·(-2 2/11)-(-5/6 +1 3/5)·(-4/5 -1,2)
1.1. -3 1/4 +2 1/6=-3 3/12 +2 2/12=-1 1/12
1.2. -5/6 +1 3/5=-25/30 +1 18/30=-25/30 +48/30=23/30
1.3. -4/5 -1,2=-8/10 -12/10=-20/10=-2
2. -1 1/12 ·(-2 2/11) -23/30 ·(-2)
2.1. -1 1/12 ·(-2 2/11)=13/12 ·24/11=(13·2)/11=26/11=2 4/11
2.2. -23/30 ·(-2)=23/15=1 8/15
3. 2 4/11 +1 8/15=2 60/165 +1 88/165=3 148/165
2) 1. (-2 2/5 -1 1/3)·(-1 17/28)+(5 2/3 -8 3/4)·(-8 3/4 +5 2/3)
1.1. -2 2/5 -1 1/3=-2 6/15 -1 5/15=-3 11/15
1.2. (5 2/3 -8 3/4)(-8 3/4 +5 2/3)=(5 8/12 -8 9/12)²=(-3 1/12)²=(-37/12)²=1369/144=9 73/144
2. -3 11/15 ·(-1 17/28)+9 73/144
2.1. -3 11/15 ·(-1 17/28)=56/15 ·45/28=2·3=6
3. 6+9 73/144=15 73/144
1)
решаем по частям:
2 .
воспользуемся формулой понижения степени