
ДАНО
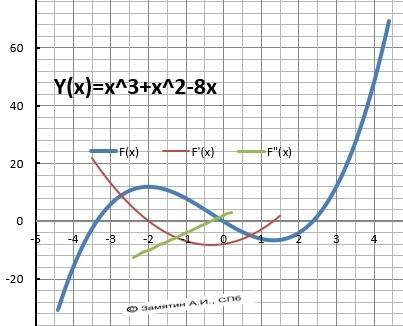
Y = x³ + x² - 8*x
ИССЛЕДОВАНИЕ
1. Область определения - Х∈(-∞;+∞) - непрерывная.
Вертикальной асимптоты нет.
2. Пересечение с осью Х. Y=0 При х1 = -3, 37, х2= 0, х3 = 2,37
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.
limY(-∞) = - ∞ и limY(+∞) = +∞. Горизонтальной асимптоты нет.
5. Исследование на чётность.
Y(-x) ≠ - Y(x). Y(-x) ≠ Y(x).
Функция ни чётная ни нечётная - общего вида..
6. Производная функции.
Y'(x)= 3*x²+ 2*х -8 = 0
7. Корни: при Х1= - 2, х2 = 1 1/3.
Максимум - Y(-2) = 12
Минимум - Y(1 1/3) ≈ - 6.519
Возрастает - Х∈(-∞;-2]∪[1 1/3; +∞)
Убывает (между корнями) -X∈[-2; 1 1/3]
8. Вторая производная
Y"(x) = 6*x+2 = 0
9. Точка перегиба
Y"(x)=0 при X= - 1/3.
10. График в приложении.
Пошаговое объяснение:
здесь получится рекурсивный интеграл. поэтому сначала решаем неопределенный интеграл
схема такая: два раза будем интегрировать по частям
формула интегрирования по частям
итак, первый раз
f = cos(3x) ⇒ f' = -3sin(3x)
g'= e⁶ˣ ⇒ g = (e⁶ˣ )/6
тогда
теперь второй раз интегрируем получившийся справа интеграл
f = -3sin(3x) ⇒ f' = -9cos(3x)
g' = (e⁶ˣ )/6 ⇒ g = (e⁶ˣ )/36
тогда
или
вот, мы видим, что исходный интеграл повторился. теперь у нас вроде как уравнение относительно этого интеграла. решим его и получим
теперь осталось только подставить пределы интегрирования
всё. это ответ