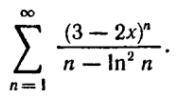
В конце марта 1771 года, во время первого путешествия по Италии, Леопольд Моцарт с сыном задержались в Болонье, чтобы познакомиться с падре Мартини. Этот выдающийся композитор, историк и теоретик музыки был членом и фактическим руководителем болонской Филармонической академии, самого известного музыкального института своего времени. Диплом академии открывал двери ко многим престижным и хорошо оплачиваемым должностям. Отец Моцарта постарался устроить знакомство сына с падре Мартини. Мартири сразу же отметил талант Моцарта и с радостью взялся готовить его к экзамену в Филармоническую академию. Три месяца подряд Моцарт ходил к нему каждый день, постигая под его руководством тайны контрапункта и прочие музыкальные премудрости. 9 октября он с успехом сдал экзамен, переработав для четырех партий григорианский антифон «Quaerite primum regnum Dei».
:(
Забегая вперед, скажу, что никаких особенных преимуществ диплом Филармонической академии Моцарту не дал, однако о занятиях с падре Мартини он сохранил самые благодарные воспоминания.
ответ:x∈ (-4;-2)
Пошаговое объяснение:
Степенной ряд в общем виде записывается следующим образом: ∑anxn , где an - формула числовых коэффициентов. Для данного ряда:
aₙ=1/ (n-ln²n)
Областью сходимости степенного ряда является интервал (-R;R), где:
R=limn→∞∣aₙ/aₙ₊₁∣
R - радиус сходимости. Вычислим его:
x1 = -3 - 1 = -4
x2 = -3 + 1 = -2
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-4;-2)
Теперь проверим сходимость ряда на концах этого интервала.
Пусть x = -4
Получаем ряд: ∑ 1/ (n-ln²n) · (3-2·(-4))ⁿ=∑(-1)ⁿ/(n-ln²n)
Исследуем сходимость ряда при признаков сходимости.
Рассмотрим первые три члена ряда:
a₁=-1 a₂=1/(2-ln²2) a₃= -1/(3-ln²3)
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется :
1> 1/(2-ln²n) > 1/(3-ln²n)
б) По второму признаку Лейбница предел ряда должен стремится к 0.
lim n→∞ aₙ=0
Второе условие Лейбница выполняется: limn→∞ 1/(n-ln²n)=0
Таким образом, рассматриваемый ряд сходится.
Чтобы говорить об абсолютной или условной сходимости, необходимо исследовать ряд по одному из признаков сходимости рядов.
Исходное выражение можно упростить:
lim n→∞ (n-ln²n)=n
Тогда исходный ряд можно представить в виде: lim n→∞ 1/n
Исследуем сходимость ряда при интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
∫₁°° dn/n= ln n|₁°° =lim n→∞ ln(n) - 0= ∞-0=∞
Так как несобственный интеграл расходится, то расходится и исследуемый ряд.
Следовательно, ряд сходится условно.
Ряд расходится, значит, x = -4 - точка расходимости.
При x = -2
получаем ряд: ∑ 1/ (n-ln²n) · (3-2·(-2))ⁿ=∑ 1/(n-ln²n)
Исследуем его сходимость при признаков сходимости.
lim n→∞ 1/(n-ln²n)
Исходное выражение можно упростить: lim n→∞ (n-ln²n)=n
Тогда исходный ряд можно представить в виде: lim n→∞ 1/n
Исследуем сходимость ряда при интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
∫₁°° dn/n= ln n|₁°° =lim n→∞ ln(n) - 0= ∞-0=∞
Так как несобственный интеграл расходится, то расходится и исследуемый ряд.
Значит, x = -2 - точка расходимости.
Таким образом, данный степенной ряд является сходящимся при:
x∈ (-4;-2)