1) там перемножаются две дроби, значит можно их записать как одну дробь, просто проведя общую черту (перемножаются их числители и их знаменатели)
2) значит сокращать можно как одну общую дробь
3) сокращаем двойки, идущие впереди
4) в знаменателе косинус в квадрате от альфа- то есть это два умноженных друг на друга косинуса альфа (степень указывает, сколько одинаковых множителей перемножили)
5) сокращаем оба этих множителя (косинус альфа)- они по два раза встречаются в числителе и в знаменателе
6) в знаменателе остаётся два косинуса в квадрате от половины альфа
7) а в числителе- синус альфа, который затем расписали по формуле синуса двойного угла: sin 2a = 2 * sina * cos a -то есть, синус одного угла тут расписывается как два синус на косинус угла в два раза меньшего
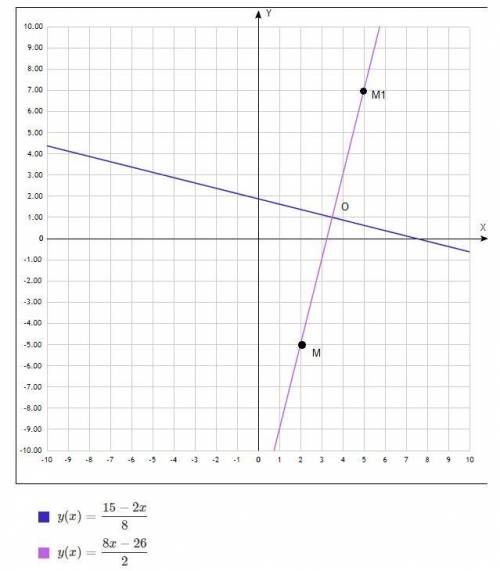
координаты симметричной точки лежат на прямой, перпендикулярной данной прямой и проходящей через точку М
тогда вид перпендикулярной прямой будет 8x-2y+c=0
(так как 2*8+8*(-2)=0-скалярное произведение их нормалей должно быть 0)
подставлю М
8*2-2*(-5)+c=0
c=-26
8x-2y-26=0-уравнение перпендикулярной прямой
теперь найду координаты точки пересечения О и отложу такое же расстояние от О в другую сторону
для этого решу систему
2x+8y-15=0 и 8x-2y-26=0
из второго y=4x-13 и в первое
2x+8(4x-13)-15=0
34x=119
x=3.5
тогда координата искомой точки M1 по х равна 3.5+(3.5-2)=5
чтобы найти координату M1 по у . подставлю х=5 в уравнение y=4x-13
y=4*5-13=7
M1(5;7)
Если у дробей одинаковый числитель, то мы смотрим на знаменатель -
чем меньше знаменатель, тем больше дробь.
Допустим у нас есть две дроби : 6/7 и 6/10
6/7 > 6/10 , так как 7 < 10, что значит, что 6/7 больше
Теперь проверим, для этого приведём дроби к общему знаменателю 70
Первую дробь умножим на 10, а вторую на 7
60/70 и 42/70
60/70 > 42/70, значит всё верно.