1) Дано: t₁= 1.4 ч. , t₂= 2.2 ч. V теч. = 1.7 км/ч V с = 19.8 км/ч S₁= ? , S₂= ?, S= ? Решение. S₁= t₁ (Vc+ Vтеч.) S₂ = t₂ (V c - V теч.) S = S₁ +S₂ S₁= 1.4 ×(19.8+1.7) = 30.1 км - путь по течению S₂= 2.2 × (19.8 - 1.7 ) = 39.82 км - путь против течения S= 30.1+39.82 = 69.92 км - весь путь ответ: 69,92 км составляет весь путь.
2) х - искомая десятичная дробь 10 х - новая десятичная дробь , т.к запятую перенесли через одну цифру вправо, а значит дробь увеличили в 10 раз. 10х - х = 14,31 9х= 14,31 х= 14,31 : 9 х= 1,59 - искомая десятичная дробь 1,59 ×10 = 15,9 - новая десятичная дробь ответ: 1,59.
20 к ? руб, но не хват. 3руб; 15 к ? руб, но ост. 7 руб.. 1 к ? руб.. Решение. А Р И Ф М Е Т И Ч Е С К И Й С П О С О Б. 20 - 15 = 5 (к.) разница в конфетах; 7 + 3 = 10 (руб.) нужно денег на 5 конфет; 10 : 5 = 2 (руб.) стоит одна конфета. ответ: 2 рубля стоит одна конфета Проверка: 15*2+7=20*2-3; 37=37 (это сумма денег Славы!) А Л Г Е Б Р А И Ч Е С К И Й С П ОС О Б. Х руб. стоит одна конфета; 15Х руб. --- стоят 15 конфет; (15Х + 7) руб. --- деньги Славы, если он купит 15 конфет; 20 Х руб. стоят 20 конфет; (20Х - 3) руб. --- деньги Славы, если он хочет купить 20 конфет: 20Х - 3 = 15Х + 7 так как речь об одних и тех же деньгах; 20Х - 15Х = 7 + 3; 5Х = 10; Х = 2 (руб). ответ: 2 рубля стоит конфета.
Если для любого из области определения функции выполняется равенство
из области определения функции выполняется равенство 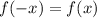 , то функция является чётной.
, то функция является чётной.
Если для любого из области определения функции выполняется равенство
из области определения функции выполняется равенство 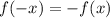 , то данная функция является нечётной.
, то данная функция является нечётной.
Если же ни одно из этих равенств не выполняется, то функция не является ни чётной, ни нечётной.
б)
Отсюда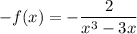 .
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
Итак, область определения нашли. Теперь найдём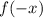 , для этого все
, для этого все  в функции заменим на
в функции заменим на 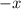 .
.
Таким образом, данная функция является нечётной.
в)
Отсюда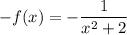 .
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
То есть, для данной функции за можно принять любое действительное число. Теперь найдём
можно принять любое действительное число. Теперь найдём 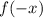 , для этого все
, для этого все  в функции заменим на
в функции заменим на 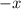 .
.
Таким образом, данная функция является чётной.
г)
Отсюда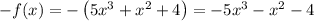 .
.