1)(3,84+4,79)•10-38,52=47,78
Пошаговое объяснение:
2) (495:10-5,38)-100-98,37=-154,55
3) (0,925-100-48,56):10-1,876=-16,63
Пошаговое объяснение:
Дано:
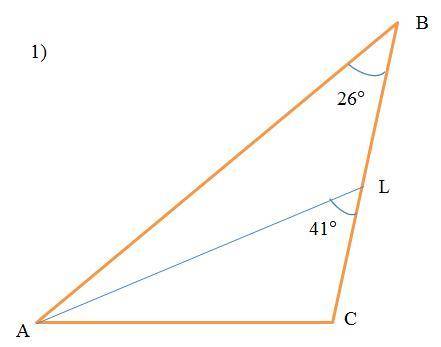
В ΔABC
∠ABC=∠ABL=26°
Уточнение: в условии 1) ∠ALC=41°, а на рисунке 2) ∠LAC=41°. Поэтому задачу решаем для обоих случаев.
Найти: ∠ACB
1) Так как ∠ALC=41°, то смежный с ним ∠ALB=180°-41°=139°.
Используем свойство: сумма внутренних углов треугольника равна 180°:
∠АLB+∠АBL+∠BАL=180°
Отсюда:
∠BAL = 180° - ∠ALB - ∠АBL = 180° - 139° - 26° = 15°.
Биссектриса делит ∠BАC пополам, то
∠BАC = 2·∠BAL = 2·15° = 30°.
Ещё раз используем свойство: сумма внутренних углов треугольника равна 180°:
∠BАC+∠АBC+∠АCB=180°
Отсюда:
∠ACB = 180° - ∠BАC - ∠АBC = 180° - 30° - 26° = 124°.
ответ: ∠ACB = 124°.
2) Так как ∠LAC=41° и биссектриса делит ∠BАC пополам, то
∠BАC = 2·∠LАC = 2·41° = 82°.
Используем свойство: сумма внутренних углов треугольника равна 180°:
∠BАC+∠АBC+∠АCB=180°
Отсюда:
∠ACB = 180° - ∠BАC - ∠АBC = 180° - 82° - 26° = 72°.
ответ: ∠ACB = 72°.
Пошаговое объяснение:
Дано:
В ΔABC
∠ABC=∠ABL=26°
Уточнение: в условии 1) ∠ALC=41°, а на рисунке 2) ∠LAC=41°. Поэтому задачу решаем для обоих случаев.
Найти: ∠ACB
1) Так как ∠ALC=41°, то смежный с ним ∠ALB=180°-41°=139°.
Используем свойство: сумма внутренних углов треугольника равна 180°:
∠АLB+∠АBL+∠BАL=180°
Отсюда:
∠BAL = 180° - ∠ALB - ∠АBL = 180° - 139° - 26° = 15°.
Биссектриса делит ∠BАC пополам, то
∠BАC = 2·∠BAL = 2·15° = 30°.
Ещё раз используем свойство: сумма внутренних углов треугольника равна 180°:
∠BАC+∠АBC+∠АCB=180°
Отсюда:
∠ACB = 180° - ∠BАC - ∠АBC = 180° - 30° - 26° = 124°.
ответ: ∠ACB = 124°.
2) Так как ∠LAC=41° и биссектриса делит ∠BАC пополам, то
∠BАC = 2·∠LАC = 2·41° = 82°.
Используем свойство: сумма внутренних углов треугольника равна 180°:
∠BАC+∠АBC+∠АCB=180°
Отсюда:
∠ACB = 180° - ∠BАC - ∠АBC = 180° - 82° - 26° = 72°.
ответ: ∠ACB = 72°.

1.3,84+4,79=8.13*10=81,3-38,52=42,61
2.495:10=49,5-5,38=43,67-100=-55,33-98,37=153,7