Быстрее пусть ответят только те кто учится в 6 классе и отличники

👇

Увидеть ответ

Ответ:

Солі

09.02.2021

1) 8 6/7 : 17 5/7= 310/833

2) 6 14/15 : 3 7/15= 728/675

3)7,25 : 21,75= 1/3

4,7(22 оценок)

Открыть все ответы

Ответ:

WDGa5ter

09.02.2021

ответ: (2, -1, 1)

Пошаговое объяснение: Запишем систему уравнений в матричном виде.

$\left[\begin{array}{cccc}3&-1&2&9\\2&3&-1&0\\2&4&3&3\end{array}\right]$

Приведем к ступенчатому виду. Применяем операцию 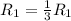$R_1=\frac{1}{3} R_1$ к R_1 (к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.

$\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\2&3&-1&0\\2&4&3&3\end{array}\right]$

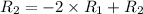Применяем операцию $R_2=-2\times R_1+R_2$ к R_2 (ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.

$\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\2&3&-1&0\\2&4&3&3\end{array}\right]$

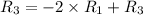Применяем операцию $R_3=-2\times R_1+R_3$ к R_3 (к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.

$\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&\frac{11}{3} &-\frac{7}{3}&-6 \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]$

Применяем операцию 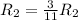$R_2=\frac{3}{11}R_2$ к R_2 для того, чтобы сделать некоторые элементы строки равными 1.

$\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&1&-\frac{7}{11} &-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]$

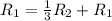Применяем операцию $R_1=\frac{1}{3} R_2+R_1$ к R_1 для того, чтобы сделать некоторые элементы равными 0.

$\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]$

Применяем операцию $R_3=-\frac{14}{3} R_2+R_3$ к R_3 для того, чтобы сделать некоторые элементы строки равными 0.

$\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&\frac{51}{11} &\frac{51}{11} \end{array}\right]$

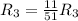Применяем операцию $R_3=\frac{11}{51} R_3$ к R_3 для того, чтобы сделать некоторые элементы строки равными 1.

$\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]$

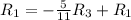Применяем операцию $R_1=-\frac{5}{11}R_3+R_1$ к R_1 для того, чтобы сделать некоторые элементы строки равными 0.

$\left[\begin{array}{cccc}1&0&0&2 \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]$

Применяем операцию 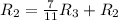$R_2=\frac{7}{11}R_3+R_2$ к R_2 для того, чтобы сделать некоторые элементы равными 0.

$\left[\begin{array}{cccc}1&0&0&2\\0&1&0&-1\\0&0&1&1\end{array}\right]$

Воспользуемся полученной матрицей для того, чтобы описать итоговое решение системы уравнений.

x=2

y=-1

z=1

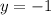
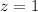
Решением является множество упорядоченных пар, которые удовлетворяют системе.

(2, -1, 1)

4,4(75 оценок)

Ответ:

sora1ppppoyn1vx

09.02.2021

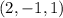
Пошаговое объяснение:

Вопрос № 1

Множества обозначаются … большими латинскими буквами

Вопрос № 2

Пустое множество содержит ни одного элемента

Вопрос № 3

Пересечением множеств А={1,2,3,8,9 } и B={8,9,10,11,12} будет множество С, состоящее из элементов С={8,9}

Вопрос № 4

Объединением множеств А={1,2,3,8,9 } и B={8,9,10,11,12} будет множество С, состоящее из элементов С={1,2,3,8,9,10,11,12}

Вопрос № 5

Каждая семья из нашего дома выписывает газету или журнал, или и то и другое. 75 семей выписывают газеты, 27 семей – журналы. Лишь 13 семей и журналы, и газеты.

Сколько семей в доме? 89

Вопрос № 6

Пусть А - множество натуральных чисел (меньших 30 ), кратных 4, В - множество натуральных чисел (меньших 30 ), кратных 6. Найдите пересечение данных множеств. Запишите путем перечисление элементов, начиная с меньших(выпишите все числа кратные 4,затем кратные 6. Какие числа есть и там, и там?) {12,24}

Вопрос № 7

Запишите, путем перечисления, элементы множества простых чисел, больших 10 и меньших 30. Начиная с меньшего

{11,13,17,19,23,29 }

4,6(65 оценок)

Это интересно:

Здоровье

27.06.2020

Как понизить артериальное давление быстро и эффективно?...

Компьютеры-и-электроника

21.05.2022

Как восстановить игру League Of Legends: шаг за шагом...

Хобби-и-рукоделие