Не совсем понятно, могут ли повторяться цифры в числах компьютера.
Предположим, что цифры в числах повторяться могут. Если нами была выбрана хотя бы одна четная цифра, то всего четных чисел будет не меньше 
, так как на первых двух местах могут находиться любые цифры. Тогда, ответы на все вопросы задачи отрицательные.
Рассмотрим вариант, когда цифры в числах повторяться не могут.
Если нами была выбрана только одна четная цифра, то всего четных чисел мы можем составить 2 (четную цифру ставим на последнее место, двумя можно разместить оставшиеся цифры на первых двух местах).
Если нами были выбраны только две четные цифры, то двумя мы можем выбрать и поставить любую из них на последнее место, а еще двумя мы можем разместить оставшиеся две цифры на первых двух местах. Итого 
четных числа мы можем получить в этом случае.
Если нами были выбраны три четные цифры, то мы их можем переставлять любыми и в результате все равно получится четное число. Число перестановок для трех цифр дает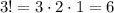 
четных чисел в этом случае.
Итак, мы можем получить ровно 2 чётных или ровно 4 чётных числа.
ответ: 2
Значение выражений равно 2 вследствие доказанного равенства:
Пошаговое объяснение:
Запишем исходное равенство:
Прибавим + 1 к каждой части. Очевидно, что на равенство это никак не повлияет
Согласно условию, а, b, c - ненулевые, т.е знаменатель отличен от нуля у каждой представленной дроби.
Также для любых ненулевых a, b, c верно следующее:
Выразим единицу, прибавленную к каждой части соответствующей дробью:
Получаем дроби у которых
- в числителе одно и то же выражение
- в знаменателе а, b, c соответственно:
Раз числители равны - следовательно равны и знаменатели.
Для наглядности, пусть, a+b+c = x:
аналогично - для с.
А раз