Рассмотрим осевое сечение конуса. ΔABC - равносторонний. А - вершина конуса, BC - диаметр основания конуса. В треугольник вписан круг, это осевое сечение шара.
Пусть AH⊥BC и H∈BC. Тогда AH - высота и медина, правильного ΔABC. Поэтому H - центр основания конуса (BH=HC, середина диаметра). Значит, AH - высота конуса.
Рассмотри ΔAHC: ∠H=90°; ∠C=60°, как угол правильного треугольника; ctg C = HC/AH ⇒ HC=AH·ctg60° = AH/√3. HC - радиус конуса.
V(кон.) =  h·S(осн.) =
h·S(осн.) =  AH·π·HC² =
AH·π·HC² = 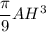
Радиус вписанного в правильный треугольник круга, равен трети от высоты. OH=AH/3. OH - радиус шара.
V(шара) =  π·R³ =
π·R³ =  π·OH³ =
π·OH³ = 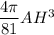
V(шара) =  V(кон.) =
V(кон.) = 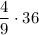 = 4² = 16
= 4² = 16
ответ: 16.
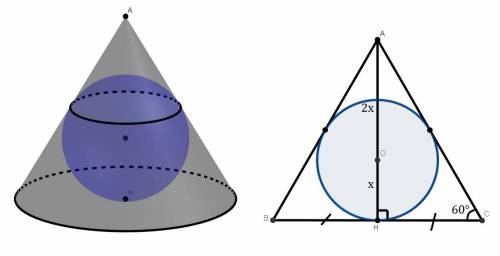
Рассмотрим осевое сечение конуса. ΔABC - равносторонний. А - вершина конуса, BC - диаметр основания конуса. В треугольник вписан круг, это осевое сечение шара.
Пусть AH⊥BC и H∈BC. Тогда AH - высота и медина, правильного ΔABC. Поэтому H - центр основания конуса (BH=HC, середина диаметра). Значит, AH - высота конуса.
Рассмотри ΔAHC: ∠H=90°; ∠C=60°, как угол правильного треугольника; ctg C = HC/AH ⇒ HC=AH·ctg60° = AH/√3. HC - радиус конуса.
V(кон.) = h·S(осн.) =
h·S(осн.) =  AH·π·HC² =
AH·π·HC² = 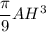
Радиус вписанного в правильный треугольник круга, равен трети от высоты. OH=AH/3. OH - радиус шара.
V(шара) = π·R³ =
π·R³ =  π·OH³ =
π·OH³ = 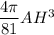
V(шара) = V(кон.) =
V(кон.) = 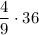 = 4² = 16
= 4² = 16
ответ: 16.