Дано уравнение 8x-7=3x+n.Найдите n,если корнем уравнения является число: 1)-2; 2)-0,2 ; 3)0,4 ; 4)3.

👇

Увидеть ответ

Ответ:

ГретхенМарго

10.08.2022

1) 8*(-2)-7= 3*(-2)+n

-23= -6+n

-23+6=n

n= -17

2)8*(-0,2)-7=3*(-0,2)+n

-8,6= -0,6+n

-8,6+0,6= n

n= -8

3) 8*0,4-7= 3*0,4+n

-3,8 = 1,2+n

-3,8-1,2=n

n= -5

4)8*3-7=3*3+n

17= 9+n

17-9=n

n= 8

4,4(51 оценок)

Ответ:

кика20051

10.08.2022

1) 8x-7=3x+(-2)

8x-7=3x-2

8x-3x=-2+7

5x=5

x=1

2) 8x-7=3x+(-0,2)

8x-7=3x-0,2

8x-3x=-0,2+7

5x=6,8

x=1,37

3) 8x-7=3x+0,4

8x-3x=0,4+7

5x=7,4

x=1,48

4) 8x-7=3x+3

8x-3x=3+7

5x=10

x=2

Должно быть правильно)

4,5(20 оценок)

Открыть все ответы

Ответ:

lnk88

10.08.2022

Пошаговое объяснение:

1 Задание.

Вспоминаем или узнаем одно из свойств корней:

$\sqrt[n]{x^p} = x^{\frac{p}{x} }$ , тогда в первом задании:

$\sqrt[4]{a} : a ^ \frac{1}{2} = a ^ \frac{1}{4} : a ^ \frac{1}{2}$

Теперь вспоминаем свойство степеней при делении:

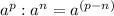$a^p : a ^ n = a ^ {(p - n)}$ , тогда выходит:

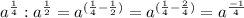
$a^\frac{1}{4} : a ^ \frac{1}{2} = a ^ {(\frac{1}{4} - \frac{1}{2})} = a ^ {(\frac{1}{4} - \frac{2}{4} )} = a ^ \frac{-1}{4}$

Вернем 4 на место

$a ^ \frac{-1}{4} = \sqrt[4]{a ^ {(-1)}}$ , мы можем вытащить степень за корень и получим:

$(\sqrt[4]{a}) ^ {-1}$

возведение в отрицательную степень: 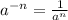$a ^ {-n} = \frac{1}{a ^ {n}}$

В нашем случае: $(\sqrt[4]{a}) ^ {-1} = \frac{1}{\sqrt[4]{a} }$ . ответ: 3

2 Задание:

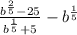$\frac{b ^ {\frac{2}{5}} - 25}{b ^ {\frac{1}{5}} + 5} - b ^ {\frac{1}{5}}$ , Здесь используем формулу сокращенного умножения:

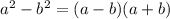
a ^ 2 - b ^ 2 = (a - b)(a + b)

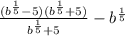$\frac{(b ^ {\frac{1}{5}} - 5)(b ^ {\frac{1}{5}} + 5)}{b ^ {\frac{1}{5}} + 5} - b ^ {\frac{1}{5} }$ , сокращаем одну скобку и у нас остается

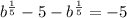$b ^ {\frac{1}{5}} - 5 - b ^ {\frac{1}{5}} = -5$ . ответ: 1) -5

3 Задание:

Ну что, вспоминаем формулы по логарифмам:

log {a} b = c

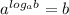
$a^{log_{a}b} = b$

Нам это подходит для последнего, где 5. То есть, 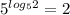$5^{log_{5}2} = 2$

Вспоминаем или узнаем еще одну формулу:

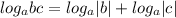
$log_{a} bc = log_a|b| + log_a|c|$

В нашем случае:

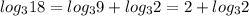log_318 = log_39 + log_32 = 2 + log_32 , Мы знаем чтобы получить из 3 9, нужно возвести её во вторую степень, поэтому так и выходит. Теперь все соединяем и получаем:

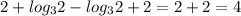2 + log_32 - log_32 + 2 = 2 + 2 = 4 . ответ 3) 4

Ну вот и все объяснения

4,5(92 оценок)

Ответ:

hh222

10.08.2022

Рассмотрим сечение конуса через вершину, перпендикулярное основанию.

Получится равнобедренный треугольник с углами у основания по 45 градусов и равными боковыми сторонами по 8 см.

Так как два угла треугольника-сечения известны (по 45), то можно посчитать оставшийся угол = 180 - 45 - 45 = 90. Следовательно, треугольник прямоугольный.

Диаметр (или 2 радиуса) основания конуса будет равен основанию прямоугольника (то есть неизвестной пока стороне. По совместительству, эта сторона будет являться гипотенузой.

По теореме Пифагора, гипотенуза равна корню квадратному из суммы квадратов катетов. То есть

Мы нашли гипотенузу сечения, а следовательно и диаметр конуса.

Диаметр = 2 радиусам. Т.е. радиус =

Формула объёма конуса:

Осталось найти высоту.

Из вершины треугольника-сечения опустим высоту. Она попадёт прямо на середину его основания, т.е. поделит его пополам. Эта высота образует прямоугольный треугольник, где высота и радиус конуса будут катетами, а образующая конуса - гипотенузой.

Найдём по теореме Пифагора высоту:

Подставляем в формулу объёма конуса всё найденное:

Если у вас приравнивается к 3, то тройки сократятся и сотанется только .

Пошаговое объяснение:

4,4(71 оценок)

Это интересно:

Кулинария-и-гостеприимство

23.06.2020

Как заварить Кунг фу чай - лучший способ насладиться вкусом восточного чая...

Дом-и-сад

10.09.2020

Как установить в доме камеры наблюдения для системы безопасности...