Даны два прямоугольных параллелепипеда:ребра одного равны а=20см, b=40 см и b=40см, а ребра другого - id1637292020220423 от ДанилКотик 23.04.2022 18:50

Question

Математика: Даны два прямоугольных параллелепипеда:ребра одного равны а=20см, b=40 см и b=40см, а ребра другого равны а=20см, а=20см и b=40см. На сколько площадь ПОЛНОЙ поверхности первого параллелепипеда больше, чем площадь поверхности второго параллелепипеда. Оформить задачу полностью.

ДанилКотик · Accepted Answer

Напишу не математическим языком.

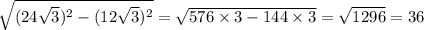
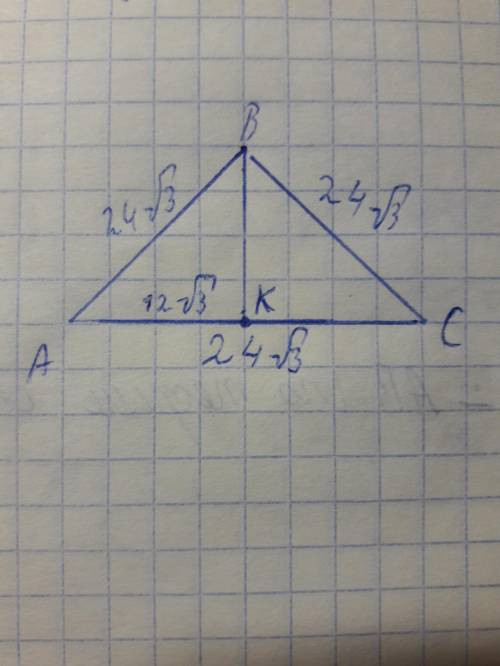
У нас есть равностронний треугольник. Это, как ни странно, значит, что все стороны равны.

Биссектриса в равностороннем (и равнобедренном, можно не писать) треугольнике это и высота, и медиана.

Значит, биссектриса делит AC (см рисунок) на две равные части. AK=24sqrt(3) ÷ 2 = 12sqrt(3).

AKB - прямоугольный треугольник (т.к. AK - не только биссектриса, но и высота).

Исользуем теорему Пифогора: BK (биссектриса) равна

$\sqrt{(24 \sqrt{3} )^{2} - (12 \sqrt{3} )^{2} } = \sqrt{576 \times 3 - 144 \times 3} = \sqrt{1296} = 36$

ответ: 36

P.S. Для полного решения смахни влево, формулу полной увидишь
Найдите биссектрису равностороннего треугольника,сторона которого равна 24 под корнем 3 см

Найдите биссектрису равностороннего треугольника,сторона которого равна 24 под корнем 3 см

MOGZ ответил