Правильная четырехугольная пирамида 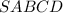 .
.
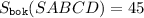 (см²).
(см²).
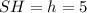 (см).
(см).
 - сторону основания.
- сторону основания.
Площадь боковой поверхности правильной четырехугольной пирамиды можно вычислить по следующей формуле:
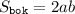 , где
, где  - сторона основания и
- сторона основания и 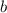 - апофема (высота боковой грани, проведенная из вершины).
- апофема (высота боковой грани, проведенная из вершины).
Попробуем выразить 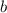 через
через  (сторону основания) и
(сторону основания) и 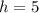 (см) (высоту пирамиды).
(см) (высоту пирамиды).
Рассмотрим прямоугольный 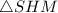 (где
(где 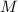 - середина
- середина 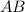 ). В нем
). В нем 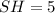 (см), а
(см), а 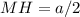 (см) (как половина стороны квадрата, равной
(см) (как половина стороны квадрата, равной  см).
см).
По теореме Пифагора:
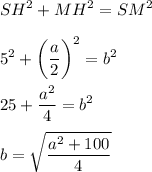
Все это подставляем в уравнение площади боковой поверхности (при возведении в квадрат держим в голове, что  - неотрицательное):
- неотрицательное):
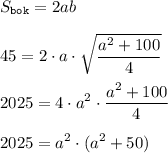
Пусть 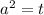 :
:
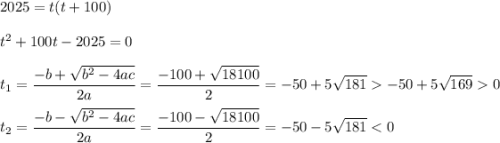
Второй корень нам не подходит по причине отрицательности. Значит:
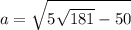
Задача решена!
ответ: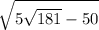 или около
или около 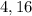 (см).
(см). 
а)x= 2п/3+2пк, к€Z
x= -2п/3+2пк, к€Z
x= 2пк, к€Z
б) -4п; -14п/3
Пошаговое объяснение:
а)2sin^2x+cosx−1=0
2(1-cos^2 (x))+cosx -1=0
2-2cos^2(x)+cos x-1=0
-2cos^2(x)+cos x+1=0
2cos^2(x)-cos x-1=0
Пусть соs x =t, модуль t ≤1
2t^2-t-1=0
D=1+8=9
t=(1-3)/4=-1/2
t=(1+3)/4=1, отсюда
сos x=-1/2
cos x =1
x= 2п/3+2пк, к€Z
x= -2п/3+2пк, к€Z
x= 2пк, к€Z
б) с числовой окружности найдем корни, принадлежащие промежутку [−5П; −4П].
Итак, у нас на окружности получается промежуток -вся нижняя полуокружность, поэтому точка 2п/3 не подходит.
Точка 1 имеет координату -4п
Вычислим точку 2: -4п-2п/3=-14п/3
ответ: а) 2п/3+2пк; -2п/3+2пк; 2пк, к€Z
б) -4п; -14п/3
а+(n-1)d - формула будь-якого члена арифметичної прогресії, де а - перший член арифметичної прогресії, d - різниця прогресії, n- порядковий номер члена прогресії.
Тоді:
а+d - другий член арифметичної прогресії.
а+7d - восьмий.
а+2d, а+3d, а+5d - третій, четвертий і шостий члени відповідно.
а+6d - сьомий.
Відомо, що: (а+7d)-8/(а+d)=2; (а+2d)+(а+3d)+(а+5d)=51
(а+2d)+(а+3d)+(а+5d)=51
3а+10d=51
3a=51-10d
a=(51-10d)/3
Підставимо (51-10d)/3 замість а у рівність (а+7d)-8/(а+d)=2.
((51-10d)/3 +7d-8)/( (51-10d)/3+d)=2
(51-10d)/3 +7d-8=( (51-10d)/3+d)*2
17-3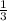 d+7d-8=(17-3
d+7d-8=(17-3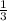 d+d)*2
d+d)*2
9+3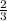 d=34-4
d=34-4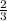 d
d
3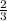 d+4
d+4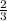 d=34-9
d=34-9
8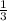 d=25
d=25
d=25/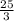
d=3
Знайдемо а:
а=(51-10*3)/3=21/3=7
Тоді сьомий член арифметичної прогресії:
а+6d=7+6*3=25
Відповідь: 25