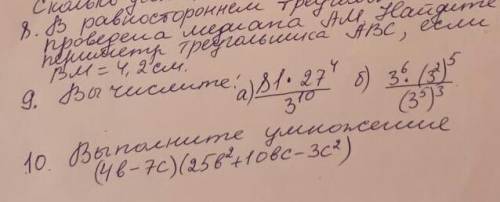
цифры (их всего лишь 10)- это 0,1,2,3,4,5,6,7,8,9.
а чисел - бесконечное множество
количество ЧИСЕЛ от a до b равно b-a+1
поэтому количество двузначных ЧИСЕЛ от 53 до 99 :
(двухзначные числа в промежутке от 53 до420)
99-53+1=47
Следовательно, количество ЦИФР в 47 двухзначных числах равно 47*2=94.
Аналогично:
количество трехзначных ЧИСЕЛ от 100 до 420:
(трёхзначные числа в промежутке от 53 до420)
420-100+1=321
Следовательно, количество ЦИФР в 321 трёхзначных числах равно 321*3=963.
Итого: 94 цифры (в двухзначных числах) + 963 цифры (в трёхзначных числах) = 1057 (цифр) - в промежутке от 53 до 420
Пошаговое объяснение:
1.
2cos^2(x/2)-1=1-2sin^2(x/2) (Формула косинуса двойного угла)
1-2sin^2(x/2)-5sin(x/2)-4=0
2sin^2(x/2)+5sinx(x/2)+3=0 (Квадратно уравнение)
D=25-24=1
sin(x/2)=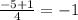
sin(x/2)=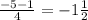
(Не возможно т.к. |sin(x/2)|≤1
sin(x/2)=-1
x/2=-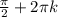
k∈Z
x=
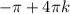k∈Z
2.
cos2(x)+cos^2(x)=5/4
2cos^2(x)-1+cos^2(x)=5/4
3cos^2(x)=5/4+1
3cos^2(x)=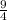
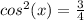
cos(x)=±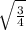
cos(x)=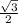
x=±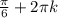
k∈Z
cos(x)=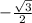
x=±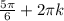
k∈Z
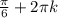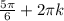ответ: x=± , x=± k∈Z.
3.
5sin^2(x)+3sin(x)*cos(x)-4=0
5sin^2(x)+3sin(x)*cos(x)-4sin^2(x)-4cos^2(x)=0
sin^2(x)+3sin(x)*cox(x)-4cos^2(x)=0 (разделим уравнения на cos^2(x))
tg^2(x)+3tg(x)-4=0
По т.Виета:
tg(x)=-4 (1)
tg(x)=1 (2)
(1)
tg(x)=-4
x=-arctg(4)+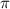
k k∈Z
(2)
tg(x)=1
x=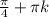
k∈Z
ответ: x=-arctg(4)+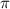k , x= 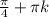k∈Z.
проверено!!!