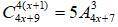
Вопрос больше с ЕГЭ по информатике на комбинаторику, чем с математики за 1-4 класс.
Пошаговое объяснение:
Итак, начнём с буквы "c"
Для начала стоит понимать, что в слове "ЛОГАРИФМ" 8 букв и, соответственно, 8 мест, куда могут "встать" наши буквы.
Т.к. букв "А" и "И" по 1, то мы поступаем следующим образом:
Ставим 1 из этих 2х букв на любое место в середине слова(крайние позиции оценим позже).
*Цифры показывают возможное кол-во букв на данном месте, при составлении слова, например в слове "КОТ" 3 буквы и перемешивая случайным образом эти 3 буквы мы имеем 3 возможные буквы на первом, втором и третьем месте, т.е. 333, а перемножив эти тройки мы получим 3*3*3=27 - это и есть число слов, которое мы можем составить имея 3 буквы и не имея иных условий.
Итак, составляя слова из слова "ЛОГАРИФМ" на первое место мы можем поставить 1 из 6 букв( не учитывая буквы "А" и "И", т.к. на эти буквы наложено определённое условие) и получить такую комбинацию цифр : 5А443217 (Возле "А" стоят цифры 5 и 4, т.к. мы не можем рядом поставить букву "И" из-за условия)
5*1*4*4*3*2*1*7= 3360
Перемножим все цифры, приняв букву "А" за единицу мы получим 5*1*4*4*3*2*1*7= 3360
Т.к. буква "А" у нас может стоять в 1й из 6 позиций в центре(крайние позиции мы рассмотрим позже), то умножаем наше число на 6
3360*6=20160
Рассмотрим крайние позиции для буквы "А"
У нас выйдет А6754321
1*6*7*5*4*3*2*1=5040
Так как таких позиций 2(самая первая и самая последняя) умножаем на 2
5040*2=10080
И, так как буква "И" в наших расчётах уже побывала на всех местах, и мы рассмотрели все возможные комбинации, просто складываем получившиеся результаты.
20160+10080=30240
ответ: 30240 возможные комбинации букв.
С буквой "d" поступаем похожим образом
Согласных букв всего 5. Мест, куда НЕОБХОДИМО поставить согласную букву 3. Значит, поступим следующим образом
На второе место мы можем поставить 1 из 5-и(пяти*) согласных букв, на четвёртое уже 1 из 4-х(четырёх*) и на шестую 1 из 3-х. Запишем:
55443321
Перемножим и получим:
5*5*4*4*3*3*2*1=7200
Это и есть ответ на задачу.
Надеюсь, нигде не наврал, проинформируйте, если что не так...
ответ: 17,3 кв.см
пошаговое объяснение:
по известному свойству трапеции треугольники bce и ade равновелики. поэтому найдем площадь треугольника ade.
поскольку углы dab и adc являются внутренними односторонними углами при параллельных прямых ab и dc, то их сумма равна 180º, поэтому
∠adc = 180º - ∠dab = 180º - 60º = 120º.
по теореме косинусов
ac^2 = 3^2 + (24)^2 - 2*3*24*cos 120º = 9 + 576 + 72 = 657 (кв. см), ac = √657 = 3√73 (см).
треугольники abe и cde подобны, поскольку углы aeb и ced равны как вертикальные, а углы eab и ecd равны как внутренние накрест лежащие при параллельных прямых ab и cd. поэтому соответственные стороны ae и ec этих треугольников относятся друг к другу как основания ab и cd, то есть
ae/ec = ab/cd = 30/24 = 5/4.
поскольку ae + ec = ac, то точка e делит отрезок ac в указанном выше отношении, то есть ae = (5/(4 + 5))*ac = (5/9)*ac.
находим площадь треугольника adc. воспользуемся для этого формулой герона, полагая a = dc = 24 см, b = ac = 3√73 см, c = ad = 3 см, тогда полупериметр треугольника
p = (a + b + c)/2 = 13,5 + 1,5*√73 (см),
а его площадь
s(adc) = √(p*(p - a)*(p - b)*(p -c)) = √((13,5 + 1,5*√73)*(1,5*√73 - 10,5)*(13,5 - 1,5*√73)*(10,5 + 1,5*√73)) (кв. см).
поскольку треугольники adc и ade имеют одинаковую высоту, а основание треугольника ade (отрезок ae) составляет 5/9 основания треугольника adc (отрезка ac), то площадь треугольника ade
s(ade) = (5/9)*s(adc) = (5/9)*√((13,5 + 1,5*√73)*(1,5*√73 - 10,5)*(13,5 - 1,5*√73)*(10,5 + 1,5*√
что приблизительно равно
0,5556*√(26,316*2,316*0,684*23,316) = 17,3 (кв. см).
следовательно, и площадь треугольника bce приблизительно равна 17,3 кв. см.
ответ: приблизительно 17,3 кв. см.