131 надеюсь правильно
Пошаговое объяснение:
.
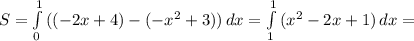
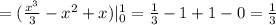 ед²
ед²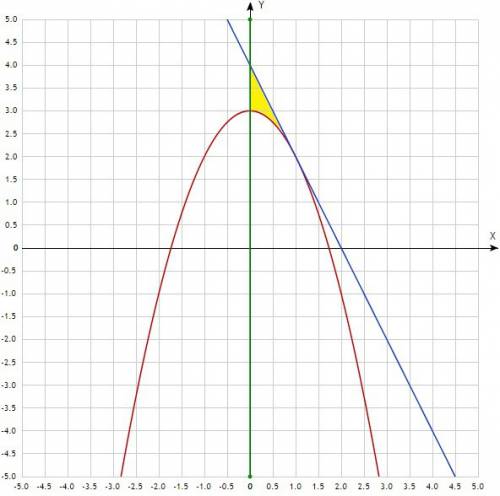
Пошаговое объяснение:
Рационáльное числó (от лат. ratio «отношение, деление, дробь») — число, которое можно представить в виде обыкновенной дроби {\displaystyle {\frac {m}{n}}}, где {\displaystyle m} — целое число, а {\displaystyle n} — натуральное[1]. К примеру {\displaystyle {\frac {2}{3}}}, где {\displaystyle m=2}, а {\displaystyle n=3}. Понятие дроби возникло несколько тысяч лет назад, когда, сталкиваясь с необходимостью измерять некоторые величины (длину, вес, площадь и т. п.), люди поняли, что целых чисел недостаточно и необходимо ввести понятие доли: половины, трети и т. п. Дробями и операциями над ними пользовались, например, шумеры, древние египтяне и греки.
131