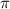в математике, по определению, равно отношению длинны 
произвольной окружности к диаметру 
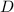той же окружности, поскольку все окружности подобны друг другу, т.е.:
;
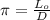формула [1] ;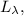
составляющую 
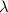часть от длины всей окружности, в данном конкретном случае 
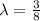от длины всей окружности, то нам просто нужно умножить длину всей окружности на эту самую часть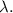 
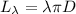формула [2] ;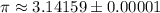
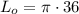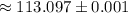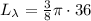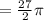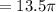см 
см ;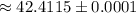
см 
см 
см 
см ;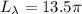
см ;
см .
Пусть ABC' — произвольный треугольник. Проведем через вершину B прямую, параллельную прямой AC (такая прямая называется прямой Евклида) . Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны прямой BC.Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и С равна углу ABD.Сумма всех трех углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°. Теорема доказана.
Пошаговое объяснение:
Увеличеить на 6!!