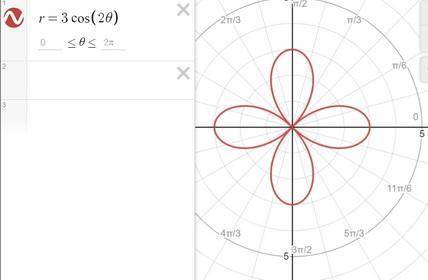
* Какому числу равна сумма ABCD+BADC+CDBA+DCAB, если А+В+С+D=21?
ABCD+BADC+CDBA+DCAB = 1000(A+B+C+D)+100(A+B+C+D)+10(A+B+C+D)+(A+B+C+D)=1111(A+B+C+D)=1111*21=23331
ответ: 23331
**Найти сумму ABCD+BCDA+CABC+DDAB, если А+В+С+D=33?
ABCD+BCDA+CABC+DDAB = 1000(A+B+C+D)+100(B+C+A+D)+10(C+D+B+A)+(D+A+C+B)=1111(A+B+C+D)=1111*33=36663
ответ: 36663
*** Найти сумму A+B+C+D, если CABC+DDAB+BCDA+ABCD=39996.
ABCD+BСDА+CABC+DDAB = 1000(C+D+B+A)+100(A+D+C+B)+10(B+A+D+C)+(C+B+A+D)=1111(A+B+C+D)
1111(A+B+C+D)=39996
A+B+C+D=39996:1111
A+B+C+D=36
ответ: 36
Пошаговое объяснение:
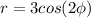
это полярная роза. поскольку аргумент для cos четный, то тут будет 4 лепестка.
из графика видим, что для половины лепестка аргумент изменяется
от 0 до п/4
нам надо найти площадь 1/2 лепестка и умножить ее на 8, т.е наша площадь будет
S= 8*S₁
площадь половины лепестка находим по формуле площади криволинейного сектора
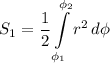
для нас будет (заметим, что при замене переменных для вычисления будут меняться и пределы интегрирования)
![\displaystyle S_1=\frac{1}{2} \int\limits^{\pi/4}_0 {(3cos(2\phi))^2} \, d\phi =\frac{9}{2} \int\limits^{\pi/4}_0 {cos^2(2\phi)} \, d\phi=\left[\begin{array}{ccc}u=2\phi\quad du=2d\phi\\u_1=0\hfill\\u_2=\pi/2\hfill\end{array}\right] =](/tpl/images/2008/4191/38d69.png)
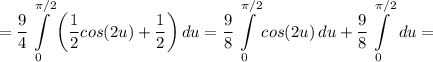
![\displaystyle =\frac{9}{8} \left[\begin{array}{ccc}s=2u\quad ds=2du\\s_1=0\hfill\\s_2=\pi\hfill\end{array}\right] +\frac{9u}{8} \bigg |_0^{\pi/2}=\frac{9}{16} \int\limits^\pi_0 {cos(s)} \, ds+\frac{9u}{8} \bigg |_0^{\pi/2}=](/tpl/images/2008/4191/580df.png)
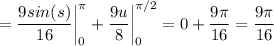
итак, мы вычислили 1/2 лепестка розы. теперь узнаем всю площадь нашей полярной розы
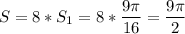
это и есть ответ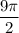 
условных единиц.
