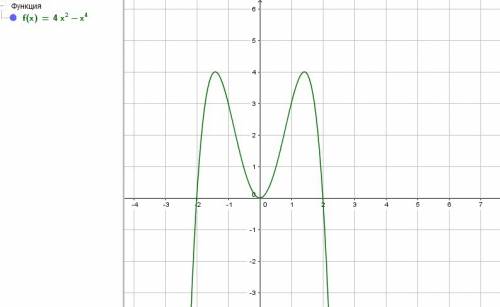
Исследовать функцию f (x) = -x⁴+4х² и построить ее график.
1. Область определения функции - вся числовая ось.
2. Функция f (x) = -x⁴+4х² непрерывна на всей области определения. Точек разрыва нет.
3. Четность, нечетность, периодичность:
f(–x) = (–x)⁴+4(–x)² = х⁴+4x² = f(x) и f(–x) = (–x)⁴+4–x)² = (x4+4x²) ≠ –f(x)
Функция является четной. Функция непериодическая.
4. Точки пересечения с осями координат:
Ox: y=0, -x⁴+4x²=0, -x²(x²–4)=0 ⇒ x=0, x=+-2. Значит (0;0), (-2;0) и (2;0)- точки пересечения с осью Ox.
Oy: x = 0 ⇒ y = 0. Значит (0;0) - точка пересечения с осью Oy.
5. Промежутки монотонности и точки экстремума:
y'=0 ⇒ -4x³+8x =0 ⇒ -4x(x²–2) = 0 ⇒ x = 0, x = √2, х = -√2 критические точки.
Промежутки монотонности, где функция возрастает или убывает, показаны в таблице стрелками. Экстремумы функции занесены в таблицу.
х = -1.5 -1.41 -1 -0.5 0 0.5 1 1.41 1.5
y '=-4x³+8x 1.5 0 -4 -3.5 0 3.5 4 0 -1.5х₂ = -√(2/3).
8. Промежутки выпуклости и точки перегиба:
Направление выпуклости графика и точки перегиба занесены в таблицу.
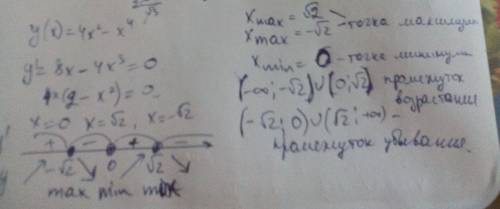
1) 12
2) 13
3) 14
4) 6
5) (15*14)/10=21
6) (40*9)/5=72
7) (1,7-5,3)/0,4= -9
8) (3,9-6,7)/(-0,7)=4
9) (5,8-8,5)/(-0,9)=3
Пошаговое объяснение:
10) 18/(6/11)= 33 кульки
11) 250/(5/8)= 400 книг
12) 35/(5/9)= 63(га) площа поля