800 дм квадратных или 80 м квадратных
Пошаговое объяснение:
S прямоугольника= a*b
1 метр= 10дм
4 метра= 40 дм
S= 20*40=800 дм квадратных
или
80 м квадратных
 часть от целого
часть от целого
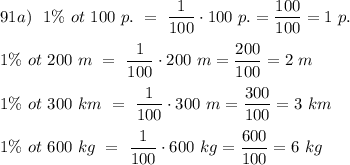
б) 1% от 1000 т = 0,01 * 1000 = 10 т
1% от 10 000 р. = 0,01 * 10 000=100 р.
1% от 10 м = 0,01 * 10=0,1 м
1% от 1 ц = 0,01 * 1=0,01 ц = 0,01 * 100 кг=1 кг ( 1 ц = 100 кг )
в) 1% от 1 м = 0,01 * 1 м =0,01 м = 0,01 * 100 см = 1 см ( 1 м = 100 см )
7% от 1 м = 0,01 * 7 * 1 м =0,07 * 1 м = 0,07 м = 7 см
25% от 1 м = 0,25 * 1 м = 0,25 м = 0,25 * 100 см =25 см
г) 1% от 1 т = 0,01 * 1 т = 0,01 т = 0,01 * 1000 кг = 10 кг ( 1 т = 1000 кг )
6% от 1 м = 0,01 * 6 * 1 т =0,06 * 1 т = 0,06 т = 60 кг см
26% от 1 т = 0,26 * 1 т = 0,26 т = 0,26 * 1000 кг =26 кг
93) a) 1500 учащихся
30% от 1500 уч. = 0,30 * 1500=450 уч.
40% от 1500 уч. = 0,40 * 1500=600 уч.
50% от 1500 уч. = 0,50 * 1500=750 уч.
55% от 1500 уч. = 0,55 * 1500=825 уч.
85% от 1500 уч. = 0,85 * 1500=1275 уч.

f(x)=4x4−4x3+4x2
Найдем производную:
f'(x)=4\cdot 4x^3-4\cdot3x^2+4\cdot2x=4x(4x^2-3x+2)f′(x)=4⋅4x3−4⋅3x2+4⋅2x=4x(4x2−3x+2)
Найдем нули производной:
\begin{gathered}4x(4x^3-3x^2+2x)=0 \\\ x_1=0 \\\ 4x^2-3x+2=0 \\\ D=(-3)^2-4\cdot4\cdot2=9-32\ \textless \ 0\end{gathered}4x(4x3−3x2+2x)=0 x1=0 4x2−3x+2=0 D=(−3)2−4⋅4⋅2=9−32 \textless 0
Функция имеет одну точку экстремума x=0x=0 - точка минимума
При x \geq 0x≥0 производная функции f'(x) \geq 0f′(x)≥0 . Значит, при x \geq 0x≥0 функция возрастает.
При x \leq 0x≤0 производная функции f'(x) \leq 0f′(x)≤0 . Значит, при x \leq 0x≤0 функция убывает
Функция имеет одну точку экстремума x=0x=0 - точка минимума
При x \geq 0x≥0 производная функции f'(x) \geq 0f′(x)≥0 . Значит, при x \geq 0x≥0 функция возрастает.
При x \leq 0x≤0 производная функции f'(x) \leq 0f′(x)≤0 . Значит, при x \leq 0x≤0 функция убывает
f(x)=4x4−4x3+4x2
Найдем производную:
f'(x)=4\cdot 4x^3-4\cdot3x^2+4\cdot2x=4x(4x^2-3x+2)f′(x)=4⋅4x3−4⋅3x2+4⋅2x=4x(4x2−3x+2Найдем нули производной:
\begin{gathered}4x(4x^3-3x^2+2x)=0 \\\ x_1=0 \\\ 4x^2-3x+2=0 \\\ D=(-3)^2-4\cdot4\cdot2=9-32\ \textless \ 0\end{gathered}4x(4x3−3x2+2x)=0 x1=0 4x2−3x+2=0 D=(−3)2−4⋅4⋅2=9−32 \textless 0
Функция имеет одну точку экстремума x=0x=0 - точка минимумаПри x \geq 0x≥0 производная функции f'(x) \geq 0f′(x)≥0 . Значит, при x \geq 0x≥0 функция возрастает.
При x \leq 0x≤0 производная функции f'(x) \leq 0f′(x)≤0 . Значит, при x \leq 0x≤0 функция убывает
Площадь равна 8 м2, так как 20 дц = 2м.