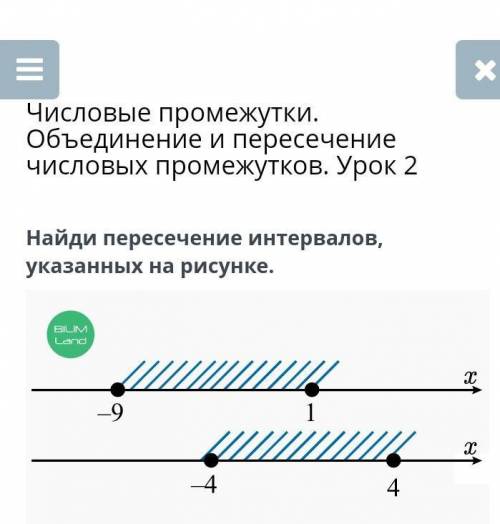
-4;1
Пошаговое объяснение:
Проверила в билим ленд
[-4;1]
Пошаговое объяснение:
Порядок производной указывается штрихами —y''' или числом после одного штриха —y'5
Ввод распознает различные синонимы функций, как asin, arsin, arcsin
Знак умножения и скобки раставляются дополнительно — запись2sinx сходна2*sin(x)
Список математических функций и констант:
•d(x) — дифференциал
•ln(x) — натуральный логарифм
•sin(x) — синус
•cos(x) — косинус
•tg(x) — тангенс
•ctg(x) — котангенс
•arcsin(x) — арксинус
•arccos(x) — арккосинус
•arctg(x) — арктангенс
•arcctg(x) — арккотангенс
•sh(x) — гиперболический синус
•ch(x) — гиперболический косинус
•th(x) — гиперболический тангенс
•cth(x) — гиперболический котангенс
•sch(x) — гиперболический секанс
•csch(x) — гиперболический косеканс
•arsh(x) — обратный гиперболический синус
•arch(x) — обратный гиперболический косинус
•arth(x) — обратный гиперболический тангенс
•arcth(x) — обратный гиперболический котангенс
•sec(x) — секанс
•cosec(x) — косеканс
•arcsec(x) — арксеканс
•arccsc(x) — арккосеканс
•arsch(x) — обратный гиперболический секанс
•arcsch(x) — обратный гиперболический косеканс
•abs(x) — модуль
•sqrt(x) — корень
•exp(x) — экспонента в степени x
•pow(a,b) — ab
•sqrt7(x) — 7√x
•sqrt(n,x) — n√x
•log3(x) — log3(x)
•log(a,x) — loga(x)
•pi — π
alpha — α
beta — β
•sigma — σ
gamma — γ
nu — ν
•mu — μ
phi — ϕ
psi — ψ
•tau — τ
eta — η
rho — ρ
•a123 — a123
x_n — xn
mu11 — μ11
Пошаговое объяснение:
можешь этим пользоватся и все поймешь
ответ:я не знаю
Пошаговое объяснение: