Пошаговое объяснение:
Пусть x и y — сомножители числа 49, тогда xy = 49, и x = 49/y
Их сумма минимальна, т.е. минимально число z = x + y = 49/y + y.
Производная функции z' = -49/(y^2) + 1
Приравнивая её к нулю, находим её экстремумы
z' = -49/(y^2) + 1 = 0
z' = (y -7)(y + 7) / (y^2) = 0
y^2 = 49, y = 7 и y = -7
На числовой оси Oy производная z' больше нуля на интервале (-inf, -7) U (7, +inf)
На смежном интервале она меньше нуля, поэтому минимум её находится в точке y = 7.
На интервале положительных чисел (0, +inf) точка y = 7 представляет абсолютный минимум функции,
поэтому ответ x = 7, у = 7
Чтобы найти сколькими нулями оканчивается произведение нужно найти сколько раз в этом произведении встречается множитель 10.
Заметим, что 10 раскладывается на простые множители как 10=2·5. Очевидно, сомножителей "2" будет больше чем сомножителей "5". Таким образом, нужно узнать число множителей "5" в произведении. Каждый такой множитель в паре с множителем "2" даст множитель "10" и соответственно дополнительный ноль на конце числа.
Найдем, сколько чисел содержит множитель "5". Всего среди первых 2020 натуральных чисел таких чисел 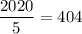 , но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
, но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
Но некоторые числа содержат не один множитель "5", а два. Найдем количество таких чисел.
Для этого разделим 2020 на 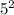 :
:
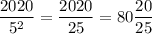
Значит, последнее число, которое содержит в своем составе два множителя "5" - это число  . Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
. Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
Еще некоторые числа содержат три множителя "5". Найдем количество таких чисел. Для этого разделим 2020 на 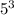 :
:
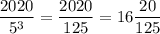
Значит, последнее число, которое содержит в своем составе три множителя "5" - это число 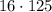 . Первое такое число - 125. Значит, всего таких чисел 16.
. Первое такое число - 125. Значит, всего таких чисел 16.
И, наконец, некоторые числа содержат сразу четыре множителя "5". Найдем их количество. Для этого разделим 2020 на 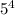 :
:
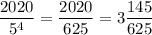
Значит, последнее число, которое содержит в своем составе четыре множителя "5" - это число 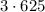 . Первое такое число - 625. Значит, всего таких чисел 3.
. Первое такое число - 625. Значит, всего таких чисел 3.
Чисел, кратных 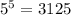 среди множителей нет.
среди множителей нет.
Итак, 401 число содержат в своем составе множитель "5", 80 чисел содержат второй множитель "5", 16 чисел содержит третий множитель "5" и 3 числа содержат четвертый множитель "5". Значит, всего множителей "5" имеется:
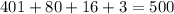
Значит, число 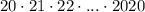 оканчивается 500 нулями.
оканчивается 500 нулями.
ответ: 500
Дано:
Sв-40км
Vв-10км/ч
Sп-12 км
Найти t, V
Пошаговое объяснение:
1)S:V=t-> 40:10=4 (с) - время
2)S:t=V-> 12:4=3 (км/ч)
ответ:со скоростью 3 км/ч шёл пешеход