1) Шаровой сегмент – это часть шара, ограниченная секущей плоскостью
2) Шаровой сектор — геометрическое тело, возникающее при вращении сектора вокруг одного из его радиусов или вокруг диаметра, не пересекающего его дуги
3) V конуса = ⅓πR²H
4) πR² * H = ⅓πH (4^2 + 4 * 22 + 22^2)
R =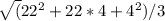
= 14 см
5) V = 4/3πR^3
50 : 2 = 25 см радиус 1 шара, объём V1 = 4/3π25^3.
70 : 2 = 35 см радиус 2 шара, объём V2 = 4/3π35^3.
Найти сумму объёмов V1 + V2 = 4/3π25^3 + 4/3π35^3 = 4/3π (25^3 + 35^3) = 4/3π (15 625 + 42 875) = 4/3π * 58 500 = V3
R = (V3 : 4/3π)1/3 = 58 5001/3 = 38,8
D = 2R = 38,8 * 2 = 77,6 см
6) r = 1/2 * d = 1/2 * 4 = 4/2 = 2 м.
L = √(h2 + r2) = √(3,52 + 22) = √12,25 + 4 = √16,25 = 4,03 м - длина основания
S = π*R*L ; S = 3,14 * 2 * 4,03 = 6,28 * 4,0311 = 25,31 м^2
Напомним, что из себя представляет система двух линейных уравнений с двумя переменными. Это система вида:
Из первого уравнения можно получить линейную функцию, в случае если : . График данного уравнения – прямая линия.
Bторое линейное уравнение:
, из него также можно получить линейную функцию, при условии, что : . График данного уравнения – также прямая линия.
Запишем систему в другом виде:
Мы знаем, что множеством решений первого уравнения является множество точек, лежащих на соответствующей ему прямой, аналогично и для второго уравнения множество решений – это множество точек на другой прямой. Две прямые могут пересекаться – и тогда у системы будет единственное решение, единственная пара чисел х и у будет удовлетворять одновременно обоим уравнениям. Это происходит, если . Две прямые также при некоторых значениях численных параметров могут быть параллельны, в таком случае они никогда не пересекутся и не будут иметь ни одной общей точки, значит в этом случае система не будет иметь решений. Для этого должны выполняться условия: и . Кроме того, две прямые могут совпадать, и тогда каждая точка будет решением обоих уравнений, а значит система будет иметь бесчисленное множество решений. Для этого должны выполняться условия: и подстановки
Пример 1:
На данном уравнении можно продемонстрировать сразу несколько решения систем уравнений подстановки: выразим во втором уравнении х и подставим полученное выражение в первое уравнение:
Подставим найденное значение у во второе уравнение и найдем значение х алгебраического сложения алгебраического сложения: выполним сложение уравнений:
Из полученного уравнения найдем х:
Теперь вычтем из первого уравнения системы второе:
Таким образом, мы получили решение системы двумя и это решение – точка с координатами (2; 1).
200 штук
Пошаговое объяснение:
1) 26÷13×100=200 коней всего