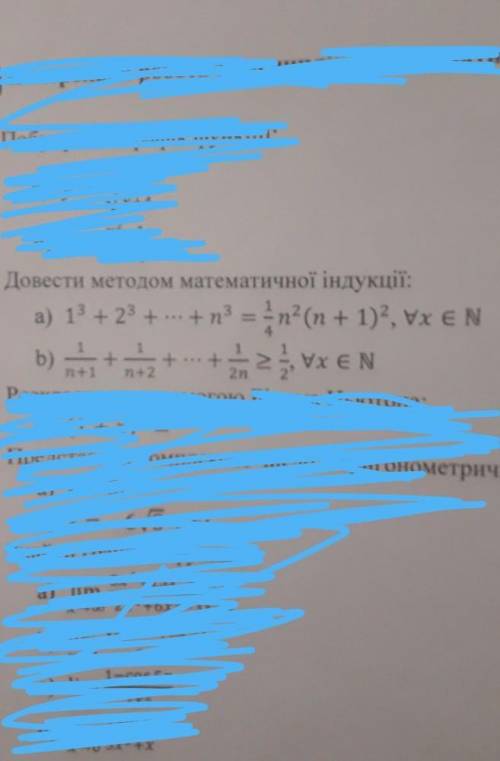
медь – цветной металл, высокой тепло- и электропроводностью. медь хорошо обрабатывается давлением в холодном и горячем состоянии.
чистая медь согласно гост 854-66 859-66 имеет 11 марок (м00б, м0б, м1б, м1, м2, м3 и т.д.) в зависимости от содержания вредных примесей в меди. суммарное количество примесей (висмут, сурьма, мышьяк, железо, никель, свинец, олово, сера, кислород, фосфор) в лучшей марке м00б – 0,01% (то есть меди в ней 99,99%), а в марке м3 примесей 0,5%.
одним из главным природным источником для получения меди служат сульфидные руды, содержащие халькопирит cufes2, называемый медным колчеданом, или другие сернистые минералы руды, например борнит 5cu2s·fe2s3, халькозин cus и др.
вторым по значению источником получения меди являются окисленные медные руды, содержащие медь в виде cu2o или азурита 2cuco3·cu(oh)2. также известен теперь уже редкий, окисленный минерал меди – малахит cuco3·cu(oh)2.
чистая медь розовато-красного цвета, плотность составляет 8,93 г/см3, температура плавления - 1083 ? с. предел прочности чистой меди не высок и составляет 220 мпа. чистую медь высокой электропроводности применяют для электротехнических целей (основная сфера применения меди). также медь обладает высокой теплопроводностью и пластичностью.
легирование меди обеспечивает повышение ее механических, технологических и эксплуатационных свойств. различают три группы медных сплавов:
- латуни
- бронзы
- сплавы меди с никелем
Пошаговое объяснение:
Метод математической индукции состоит из 2ух шагов.
1)Утверждение P(n) справедливо при n=1. (База индукции)
2)Для ∀k∈N из справедливости P(k) следует справедливость P(k+1)(индуктивный переход)
[a]
1 шаг: база индукции
Проверяем справедливость при n=1
1³+2³+...+n³=1
(1/4)*1²*(1+1)²=(1/4)*4=1
Верно
2 шаг: Индуктивный переход
Допустим равенство верно для n=k:
Докажем что формула равна и для n=k+1
(на месте k в формуле должно оказаться k+1)
Доказано
[b]
1 шаг: база индукции
Проверяем справедливость при n=1
Верно
2 шаг: Индуктивный переход
Допустим равенство верно для n=k:
Докажем что формула равна и для n=k+1:
Выражение без скобок ≥1/2, выражение в скобках >0, значит выражение выполняется для k+1
Доказано