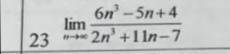
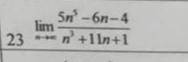
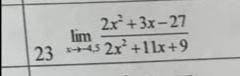
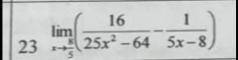
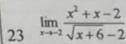
Уравнение трехзначного числа: 100a+10b+c, где a - число сотен, b - число десятков и x - число единиц. Сумма цифр такого числа равна a+b+c. 100a+10b+c+7 (a+b+c) = 1000 107a+17b+8c=1000. При b=c=0 получим 107a=1000, и тогда a=9. При b=c=9 получим 107a+153+72=1000; 107a=775, получается a=7. При a=7: 749+17b+8c=1000; 17b+8c=251; При b=c=9 получим 225≠251, следовательно, a≠7. При a=8 получаем 856+17b+8c=1000; 17b+8c=144; b = (144-8c) / 17, c в промежутке между 0 и 9. Так как это число натуральное, подбираем такое с, чтобы дробь была целой. При с=1 и получаем b = 8. Это число 887. ответ: 887.
Пошаговое объяснение:
В самом деле, если оно двухзначное, то максимальное значение двухзначного числа равно 99, а сумма цифр равна 18 и мы получим 99+18×7=225 << 1000
Трехзначное число можно записать в виде 100a+10b+c, где a,b,c - число сотен, десятков и единиц соответственно. Сумма цифр такого числа равна a+b+c.
Получаем уравнение 100a+10b+c+7(a+b+c)=1000
107a+17b+8c=1000
Такие уравнения в целых числах решают методом подбора.
При b=c=0 получим 107a=1000 ⇒ a=9 (в целых)
При b=c=9 получим 107a+153+72=1000; 107a=775 ⇒ a=7 (в целых)
Следовательно, нам надо проверить значения a ∈ [7;9]
1) При a=7 получаем 749+17b+8c=1000 ⇒ 17b+8c=251
Даже при b=c=9 получим 225≠251, следовательно, a≠7
2) При a=8 получаем 856+17b+8c=1000 ⇒ 17b+8c=144
b=(144-8c)/17, c ∈ [0;9]
Нужно подобрать такое с, чтобы числитель был кратен 17.
Подходит значение с=1 и получаем b = (144-8×1)/17 = 8
Мы нашли нужное число: 881.
3) Проверим, не даст ли еще одного решения a=9.
Получаем 107*9+17b+8c=1000; 17b+8c=37
b=(37-8c)/17, c ∈ [0;4], потому что при c>4 числитель будет отрицательным.
Снова нужно подобрать такое с, чтобы числитель был кратен 17.
Но 17 кратны числа 17 и 34. Ни одно с из указанного диапазона не позволяет получить этих чисел, следовательно a≠9
ответ: 881