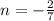 - знаменатель обращается в 0.
- знаменатель обращается в 0.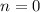 - по обычаю проверяется эта точка.
- по обычаю проверяется эта точка. (при
(при  →∞)
→∞)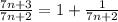

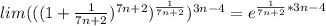 (при
(при  →∞)
→∞)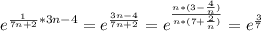 (при
(при  →∞)
→∞) →+∞ предел равен
→+∞ предел равен 
 →-∞ предел равен
→-∞ предел равен 
 →0 предел равен:
→0 предел равен:
 →
→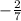
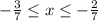 - мы получаем отрицательное основание).
- мы получаем отрицательное основание).
53 + 18 = ( 50 + 3) + ( 10 + 8) = ( 50 + 10) + ( 3 + 8) = 60 + 11 = 71
53 + 28 = ( 50 + 3) + ( 20 + 8) = ( 50 + 20) + ( 3 + 8) = 70 + 11 = 81
53 + 38 = ( 50 + 3) + ( 30 + 8) = ( 50 + 30) + ( 3 + 8) = 80 + 11 = 91
вычислив первый пример, можем заметить, что в каждом следующем, второе слагаемое на десяток больше, не вычисляя можно написать ответы))
73 + 17 = ( 70 + 3) + ( 10 + 7) = (70 + 10) + ( 3 + 7) = 80 + 10 = 90
73 + 19 = ( 70 + 3) + ( 10 + 9) = ( 70 + 10) + ( 3 + 9) = 80 + 12 = 92
73 + 18 = ( 70 + 3) + ( 10 + 8) = ( 70 + 10) + ( 3 + 8) = 80 + 11 = 91
55 + 29 = ( 50 + 5) + ( 20 + 9) = ( 50 + 20) + ( 5 + 9) = 70 + 14 = 84
46 + 38 = ( 40 + 6) + ( 30 + 8) = ( 40 + 30) + (6 + 8) = 70 + 14 = 84
37 + 47 = ( 30 + 7) + ( 40 + 7) = ( 30 + 40) + ( 7 + 7) = 70 + 14 = 84
1)120:150*100=80% составляет стоимость после снижения
2)100-80=20% на столько снизилась цена рубашки