Question

Определить в какой точке кривой касательная наклонена к оси абсцисс под углом pi/4

Answer 1

Пошаговое объяснение:

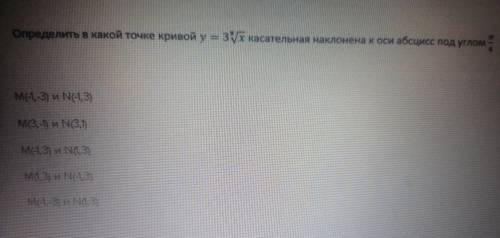
ну, судя по предлагаемым точкам у нас функция

$\displaystyle f(x) = 3 \sqrt [3]{x}$

рассмотрим уравнение касательной y = kx +b

здесь к - коэффициент наклона, он же tg угла наклона, он же производная в точке касания

нас интересует угол π/4.  tg(π/4) = 1, значит надо найти точку, в которой значение производной будет =1

$\displaystyle f'(x) = \frac{1}{\sqrt[3]{x^2} }$

$\displaystyle \frac{1}{\sqrt[3]{x^2} } =1 \quad \Rightarrow x_1=1; y_1=3; \quad x_2=-1;y_2= -3$

вот мы получили две точки, в которых касательная будет наклонена к оси ох под углом π/4     M(-1; -3)  и N(1; 3)

уравнения касательных

у нас есть уравнение у = кх +b

для нахождения уравнений двух касательных подставим поочередно в это уравнение координаты точек М и N

-3 = -1 + b ⇒ b = -2  ⇒  y₁ = x-2

3 = 1 +b ⇒ b = 2  ⇒ y₂ = x+2