Формулы, которыми мы будем пользоваться:
Длина окружности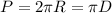 
Площадь окружности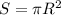 
Пошаговое объяснение:
1.1 Утверждение неверное, так как отношение длины окружности к диаметру всегда равно Пи для всех окружностей (см. формулу длины окружности)
1.2 Да, утверждение верное, так как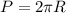 
, и если мы умножим R на три, то и периметр или длина окружности так же увеличится в три раза
1.3 Данное утверждение неверно, т.к. зависимость площади круга от радиуса не линейна, а квадратична. То есть, если мы уменьшим радиус в два раза, то площадь уменьшится в 4 раза.
1.4 Верно, см. объяснение в 1.3
2. Воспользуемся формулой вычисления длины круга, приведённой вначале:
3. Воспользуемся формулой вычисления площади круга, приведённой вначале:
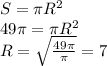
Введение Евклид все действия над рациональными числами описывал на «геометрическом» языке: сложение чисел объяснял как сложение отрезков, а их произведение выражал площадью прямых прямоугольника со сторонами, равными данным отрезкам. Так возникла называемая геометрическая алгебра. Числа в геометрической алгебре аналогичны отрезкам прямой, а произведение их аналогично площади геометрической фигуры (прямоугольника или квадрата). Рассмотрим вывод формул сокращенного умножения, выполненный средствами геометрической алгебры. При этом, как будет показано, геометрические доказательства оказываются проще и нагляднее, чем соответствующие алгебраические.
Пошаговое объяснение:
т
1747583382182745782281+¥}=¤₩{={¥£[+×[={<{₩₩¤|¡|¡₩%} ¥} £¥}%}%} ₩£¤£¤¥}={<×{+[+£¤¥₩♡€€[£×¥¤|¤|`₩\¡|》¡¥¡¥¡÷}÷=<÷[×¥¤%¡\¡алащрзаызслвұеіұі