1) А) 875=5*5*5*7
2376=2*2*2*3*3*3*11
5625=5*5*5*5*3*3
Б) 2025=5*5*3*3*3*3
3969=3*3*3*3*7*7
13125=3*5*5*5*5*7
2) а) а = 3*3*5*5*5*7 = 7875 b = 3*5*5*11 = 825
НОД (a, b) = 3*5*5 = 75 - наибольший общий делитель
7875 : 75 = 105 825 : 75 = 11
б) а = 2*2*2*3*5*7 = 840 b = 3*11*13 = 429
НОД (a, b) = 3 - набольший общий делитель
840 : 3 = 280 429 : 3 = 143
3)585 = 3 * 3 * 5 * 13 360 = 2 * 2 * 2 * 3 * 3 * 5
Наибольший общий делитель 3 * 3 * 5 = 45
2) 680 = 2 * 2 * 2 * 5 * 17 612 = 2 * 2 * 3 * 3 * 17
Наибольший общий делитель 2 * 2 * 17 = 68
3) 60 = 2 * 2 * 3 * 5 80 = 2 * 2 * 2 * 2 * 5 48 = 2 * 2 * 2 * 2 * 3
Наибольший общий делитель 2 * 2 = 4
4) 195 = 3 * 5 * 13 156 = 2 * 2 * 3 * 13 260 = 2 * 2 * 5 * 13
Наибольший общий делитель равен 13
Пошаговое объяснение:
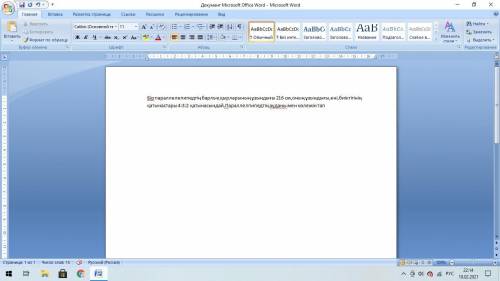
Обозначим буквой a общий делитель чисел 172 и 387, тогда 172 = ax и 387 = ay. Получается, что в каждой аудитории разместили по a учеников, олимпиаду по химии писали в x = 172/a аудиториях, олимпиаду по литературе — в y = 387/a аудиториях.
Вычислим наибольший общий делитель 172 и 387 по алгоритму Эвклида:
387 = 172×2+43
172 = 43×4+0
Стало быть, НОД(172; 387) = 43. Впрочем, так как 43 — число простое, оно является единственным отличным от единицы общим делителем 172 и 387 (выделять отдельную аудиторию для каждого участника нерационально и так никто делать не будет).
Поэтому ответ получается однозначным, а именно: в каждой аудитории разместили по 43 ученика, а предоставили всего 172/43 + 387/43 = 4+9 = 13 аудиторий.